Wir haben hier ein Zweikörperproblem. Die Dgl. für die erste Masse lautet
$$ (1) \quad m_1 \ddot x_1 = -\gamma \frac{m_1 \ m_2}{ |x_1 -x_2|^3} (x_1 - x_2) $$ und für die zweite
$$ (2) \quad m_2 \ddot x_2 = \gamma \frac{m_1 \ m_2}{ |x_1 -x_2|^3} (x_1 - x_2) $$ wobei \( \gamma \) die Gravitationskonstante ist.
Diese Gleichungen kann man vereinfachen in dem man sie einmal addiert und einma subtrahiert.
Durch Addition folgt
$$ (3) \quad m_1 \ddot x_1 + m_2 \ddot x_2 = 0 $$ und durch Subtraktion
$$ (4) \quad \ddot x_1 - \ddot x_2 = -\gamma \frac{m_1 \ m_2 }{ |x_1 - x_2 |^3} (x_1 - x_2) $$ und mit \( r = x_1 - x_2 \) folgt
$$ (5) \quad \ddot r = -\gamma \frac{m_1 \ m_2}{ |r|^3} r $$
Betrachtet man nur die Bewegung in x-Richtung, d.h. es gibt keine Geschwindigkeiten in y- bzw. z-Richtung, dann bekommt man aus (5) die Dgl.
$$ (6) \quad \ddot r = -\gamma \frac{M}{r^2} $$ mit \( M = m_1 + m_2 \) und den Anfangsbedingungen \( r(0) = r_0 \) und \( \dot r(0) = v_0 \)
Gleichung (6) ist von der Form \( y'' = f(y) \) für die es Standard Lösungsmethoden gibt. Wendet man diese an, bekommt man folgendes, für eine beliebige Konstante \( E \)
$$ (7) \quad \dot r(t) ^2 = 2 \gamma \frac{M}{r(t)}+2E $$ Aus den Anfangsbedingungen folgt $$ \dot r(0)^2 = v_0^2 = 2 \gamma \frac{M}{r_0} + 2E $$ also
$$ (8) \quad \dot r(t) = \sqrt{ 2 \gamma M \left( \frac{1}{r(t)} - \frac{1}{r_0} \right) + v_0^2 } $$
Aus Gleichung (7) folgt $$ \frac{1}{2} \dot x^2 - \gamma \frac{M}{r} = E $$ Das ist im Prinzip der Energieerhaltungssatz. Setzt man hier die Energie \( E = 0 \) bekommt man die Fluchtgeschwindigkeit $$ \dot r_F = \sqrt{ \frac{ 2 \gamma M }{ r_0 } } $$
Ist jetzt hier \( m_1 \) die Masse der Erde und \( m_2 \approx 0 \) und \( r_0 \) der Erdradius bekommt man als Fluchtgeschwindigkeit $$ \dot r_F \approx 11.18 \frac{km}{s} $$
Um die Entfernung und Geschwindigkeit über der Zeit zu plotten, muss man entweder die Dgl. (8) numerisch lösen oder folgendes Dgl. System, äquivalent zu (6)
$$ (9) \quad \begin{cases} \dot r = v \\ \dot v = -\gamma \frac{M}{r^2} \\ r(0) = r_0 \text{ und } \dot r(0) = v_0 \end{cases} $$
Ich habe (9) benutzt um die folgenden Grafiken zu erzeugen
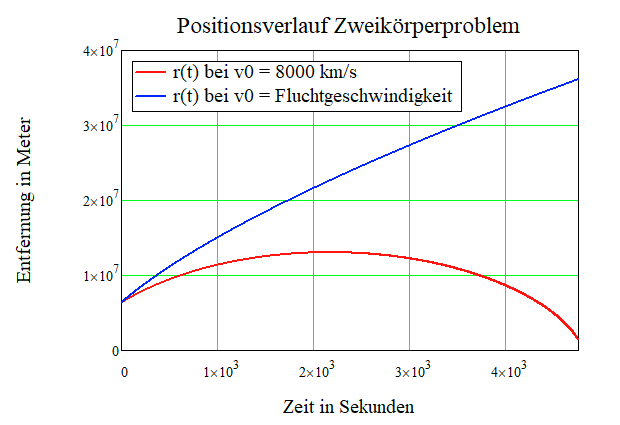
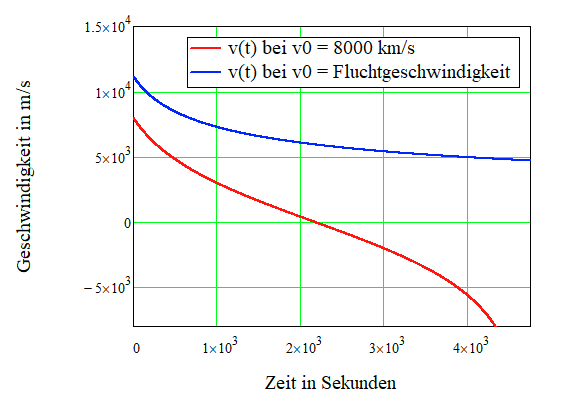
Bei einer Anfangsgeschwindigkeit kleiner als die Fluchtgeschwindigkeit wird die Geschwindigkeit der kleineren Masse irgendwann mal Null. Bei der Fluchtgeschwindigkeit konvergiert die Geschwindigkeit der kleineren Masse gegen Null für \( t \to \infty \)
Aus Gleichung (3) kann man übrigens den Schwerpunktsatz ableiten, der besagt das der Schwerpunkt zwischen den beiden Massen eine lineare Geschwindigkeit besitzt.