Haltekraft Berechnungen

Question

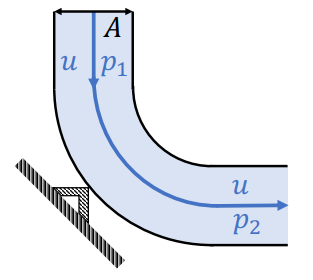
Der in der Abbildung dargestellte Rohrkrümmer wird von einem Fluid der Dichte \( \rho \) durchströmt. Der Rohr-querschnitt ist überall konstant und die Strömung ist stationär. Wie groß ist die notwendige Haltekraft, um den Krümmer ortsfest zu halten?

Gegeben: \( p_{1}, p_{2}, u, A, \rho \)

Mine Lösungen:

Haltekraft über Impulsbilanz:
$$ \int \limits_{A_{0}} \rho * \boldsymbol{u} * \boldsymbol{u} * d \boldsymbol{A}+\int \limits_{A_{0}} p * d \boldsymbol{A}=\boldsymbol{F} $$
Erster Term (konvektiver Impulsstrom)
$$ \int \limits_{A_{0}} \rho * \boldsymbol{u} * \boldsymbol{u} * d \boldsymbol{A}=\rho *\left(u_{}^{2} * A_{} *\left(e_{x}\right)+u_{}^{2} * A_{} *\left(\sin \beta * e_{y}+\cos \beta * e_{x}\right)\right)= $$

\( =\rho *\left(u_{}^{2} * A_{}\left[\begin{array}{c}-1 \\ 0\end{array}\right]+u_{}^{2} * A_{}\left[\begin{array}{c}\cos \beta \\ \sin \beta\end{array}\right]\right) \)

Zweiter Term (Druckterm des Impulses):
\( \int \limits_{A_{}} p * d \boldsymbol{A}=\int \limits_{A_{}} p_{0} * d \boldsymbol{A}+\int \limits_{A_{}} p_{1}-p_{0} * d \boldsymbol{A}_{}=\left(p_{1}-p_{0}\right) * A_{} *\left(e_{x}\right)= \)

habe ich die Aufgabe bis dahin richtig gelösst?

Gruß

F_Haltekraft = Erster Term (konvektiver Impulsstrom)  + Zweiter Term (Druckterm des Impulses)

Comments

Hallo
deine Formel mit u*u verstehe ich nicht du hast am Anfang u=uy. am Ende u=ux und musst die Änderung des Impulses ausrechnen.
was soll denn dein Winkel beta sein?
Gruß lul

---

eigentlich hies es u1*u2 aber ich habe ja nur u den u1=u2 bei  mir ist. beta ist ja 90 Grad.

Ehrlich gesagt ich habe es so versucht wie ich es verstanden habe, anscheinend habe ich alles falsch.. wie soll ich es jetzt berechnen

Kannst du mir bitte helfen.

Gruß

Answer 1

Hallo

 leider kenne ich den Ausdruck konjektiver Impulsstrom nicht,

soll u1*u2 ein Skalarprodukt sein oder ein Kreuzprodukt oder?? was sich sehe: der Impuls pro zeit  im oberen Teil geht nur in y Richtung, also A*|v|*v*ρ mit v=u*(0,-1) (positive y- Richtung nach oben) also p1*t=A*ρ*u^2*(0.-1)  entsprechend unten p2*t =A*ρ*u^2*(1,0)

die Impulsänderung  pro Zeit =Kraft ist dann p2-p1=A*ρ*u^2*(1,1), die nötige Gegenkraft also F=-A*ρ*u^2*(1,1)

mit dem Druck kann ich leider nichts anfangen, da ich schon nicht einsehe, wie es zu p1 und p2 kommt. soll das der statische Druck der Flüssigkeit sein?

Gruß lul

Comments

Hallo,

u1*u2 ist ein skalarprodukt also u1 mal u2. U ist die  Geschwindigkeit.

Druck ist vorgegeben einfach als p1 und p2.

man muss nicht druck p und Geschwindigkeit u berechnen.

Also weil druck p und geschwindigkeit u gegeben ist brauchen wir kein Massenbilanz und Bernoulligleichung aufstellen... Daher habe ich diesen schritt übersprungen und habe mit  impulsbilanz weiter gemacht... und Impulsbilanz bin mir leider nicht sicher?

Der Impuls pro Zeit wird doch einfach umgelenkt, er beträgt vorher bzw. nachher
\( \dot{\vec{p}}_{\mathrm{vor}}=\left(\begin{array}{c}0 \\ -\rho A u^{2}\end{array}\right), \quad \dot{\vec{p}}_{\mathrm{nad}_{1}}=\left(\begin{array}{c}\rho A u^{2} \\ 0\end{array}\right) \)
Der Kraftbetrag ergibt sich aus der Differenz, also
\( |\overrightarrow{\boldsymbol{F}}|=\left|\dot{\vec{p}}_{\mathrm{nach}}-\dot{\vec{p}}_{\mathrm{vor}}\right|=\dots \)

F=-A*ρ*u2*(1,1)

Gruß