Hallo Melly,
Text erkannt:
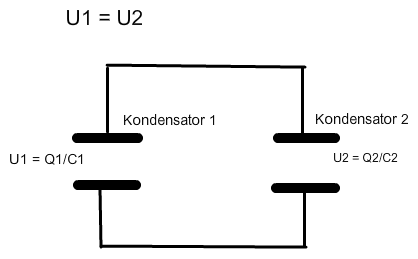
\( \cup 1=\cup 2 \)
\( \mathrm{U}_{1}=\mathrm{Q}_{1 / \mathrm{C} 1} \)
---------------------------------------------------------------------------------
C1 = 20 · 10-12 F , C2 = 50 · 10-12 F
Gesamtladung Q = U · C1 = 3000 V · 20 · 10-12 F = 6 · 10-8 C
Nach dem Ladungsausgleich muss an beiden Kondensatoren die gleiche Spannung anliegen und die Gesamtladung Q bleibt erhalten:
\(\dfrac{Q_1}{C_1}=\dfrac{Q_2}{C_2}\) und \(Q_1 + Q_2 = Q\)
\(Q_1·C_2 = Q_2·C_1\) und \(\color{green}{Q_2=Q-Q_1}\)
Q2 in die erste Gleichung einsetzen:
\(Q_1·C_2 = (\color{green}{Q-Q_1})·C_1\)
\(Q_1·C_2 = Q·C_1-Q_1·C_1\)
\(Q_1·(C_2+C_1) = Q·C_1\)
\(\color{green}{Q_1=\dfrac{Q·C_1}{C_1+C_2}}\)
Gruß Wolfgang