also ich habe gerade was komisches gemacht, und keine ahnung ob das stimmt. aber laut wolfram ist mein ergebnis dasselbe wie in der musterlösung. nur ich komme irgendwie nicht auf die umformung.
also v_0 ist ja offensichtlich Geschwindigkeit. Aber eine frage zuvor war die Eigenfrequenz und irgendwie wird es auch v_0 geschrieben und hat mich kurz irritiert.
dazu ist erstmal eine teilfrage nötig unzwar hier musste ich x(t) berechnen:

Also ganz normal Dgl aufstellen und das Ergebnis ist:
$$ x=\frac{v_{0}}{2} \sqrt{\frac{3 m}{c}} \sin (2 \sqrt{\frac{c}{3 m}} t) $$
und nun das eben für x oben eins. also für x in R= 2/3 cx und mit N = mg:
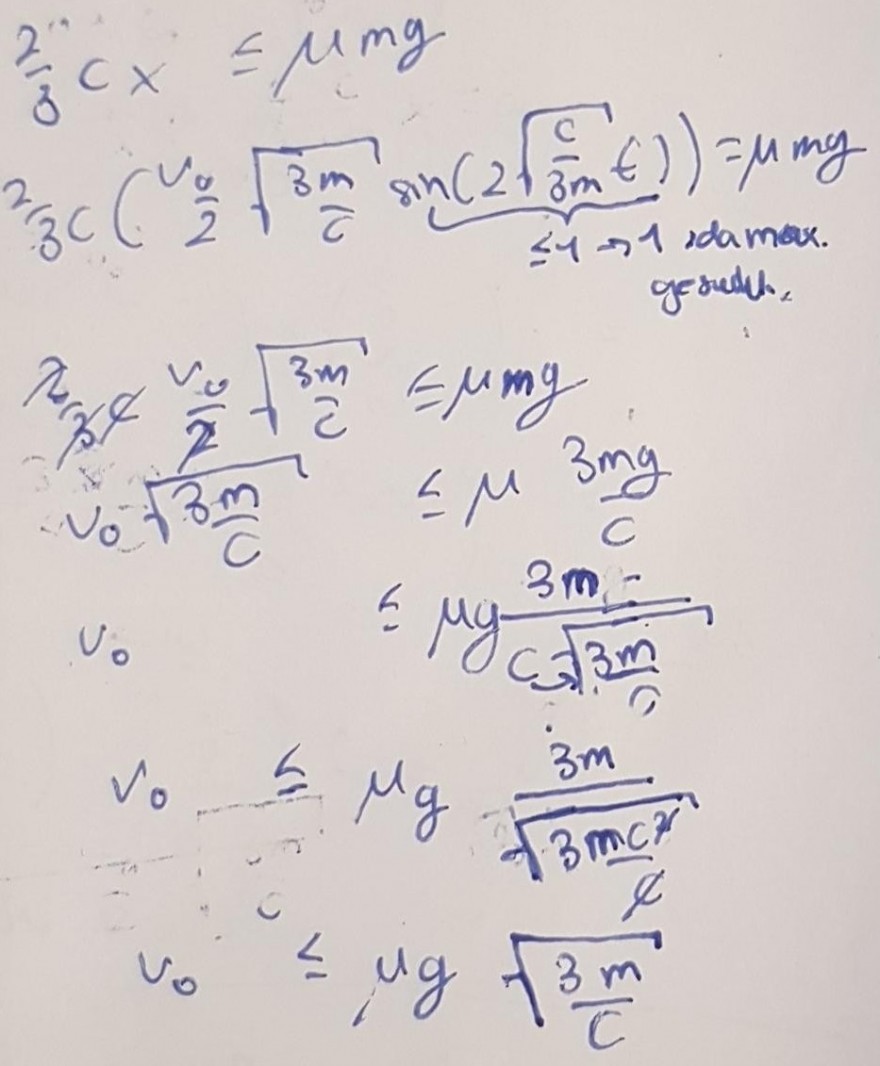
ich komme irgendwie nicht auf die letzte umformung. aber wolfram sagt diese funktionen sind dasselbe.
mfg