korrigierte Antwort
Hallo Akin,
Ich schrieb:
Das Fahrrad dreht sich genau dann um die Hinterachse, wenn das Moment um diese positiv wird.
das wäre richtig, wenn die Hinterachse irgendwo festgemacht wäre. Das ist sie aber nicht! Das ganze Fahrrad kippt vielmehr um den Punkt \(D\) (s. Skizze), bei dem das Hinterrad den Boden berührt.
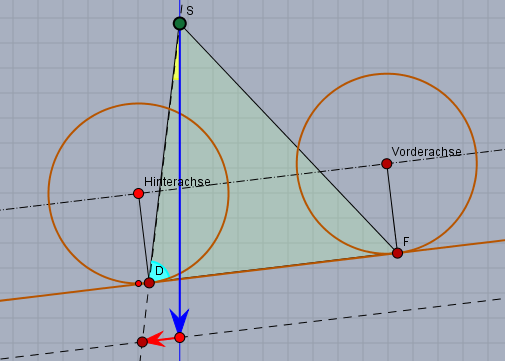
Und damit das ganze Fahrrad kippt, muss die in der Skizze rot eingezeichnete Kraft aus der Beschleunigung \(a\) so groß sein, dass die Vektorsumme aus \(a\) und \(g\) (Erdbeschleunigung blau) links von \(DS\) liegt. Der Schwerpunkt \(S\) liegt \(24,5 \text{cm}\) vor der Hinterachse und ca. \(65,6 \text{cm}\) oberhalb der Verbindungsgeraden der beiden Achsen. Daraus lassen sich dann die Strecken \(|DS|\) und \(|FS|\), sowie der Winkel \(\beta = \angle FDS\) (hellblau) berechnen: $$|DS| \approx 104,5 \text{cm} \\ |FS| \approx 126,6\text{cm} \\ \beta \approx 76,44° $$Der gelbe Winkel \(\alpha\) ist dann $$\alpha = 90°-\beta - \varphi$$wenn \(\varphi\) der Winkel der Steigung ist. Wahlweise eben $$\varphi(0\%) = 0° \\ \varphi(12\%) = \arctan(0,12) \approx 6,84°$$Betrachtet man das Dreieck, welches durch die beiden Beschleunigungen \(a\) und \(g\) aufgespannt wird, so folgt aus dem Sinussatz:$$a_{\max} = \frac{\sin \alpha}{\sin \beta} \,g$$Ich erhalte$$a_{\max} (0\%) \approx 0,25\, g \\ a_{\max} (12\%) \approx 0,12\,g$$ Gruß Werner