Hallo Leute,
ich kann eine Übung einfach nicht lösen, da ich immer knapp am Ergebnis vorbei bin.
Und zwar ist die Aufgabe folgende:
Wie soll R1 aussehen, um Rges = 20 Ohm ist?
Hier ist der Schaltskizze:
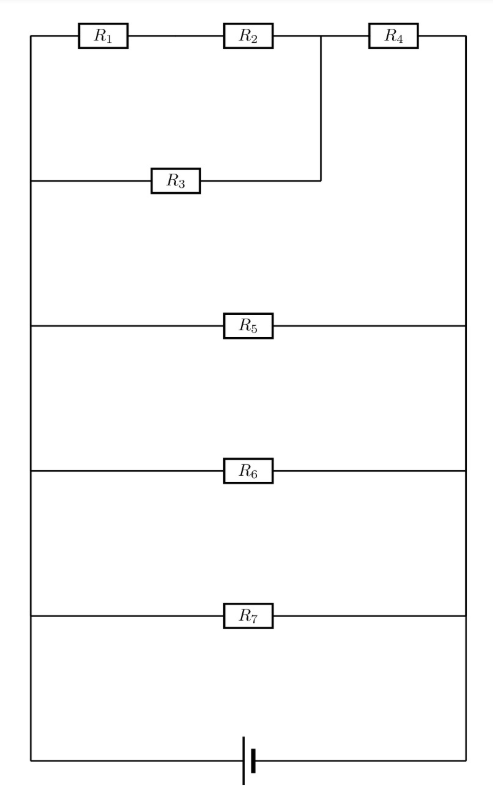
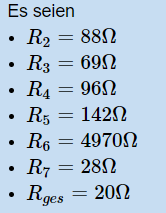
Die Formel, die ich hergeleitet habe aus dem Diagramm ist folgende:
(((R1 + R2) || R3) + R4) || R5 || R6 || R7 = 20 Ohm
bzw
(((x + 88) || 69) + 96) || 142 || 4970 || 28 = 20 Ohm
Ab hier bekomme ich sehr krumme Ergebnisse, wie z.B 18,87... oder 20,62.... aber nie 20 (wahrscheinlich wegen dem Kehrwert)
Kann mir jemand sagen, wie genau ich hier vorgehen muss, weil mit Äquivalenzumformung habe ich versucht aber jedoch immer falsch.
So hatte ich das gemacht:
(((x + 88) || 69) + 96) || 1420/61 = 20 Ohm |- (1420/61)
<=> (( x + 88) || 69) + 96 = - 200/61 Ohm |- 96
<=> (x + 88) || 69 = - 6056/61 Ohm |- 69
<=> x + 88 = - 10265/61 Ohm |- 88
<=> x = - 15633/61 Ohm = - 256,2787 Ohm
Wenn ich das aber für x einsetze, kommt nie 20 raus.
Meine Frage ist:
1) Ist meine Anfangsformel richtig?
2) Rechne ich richtig?
3) Wenn 1) und 2) stimmt, ist mein Endergebnis richtig?
Wenn nein, bitte korrigiert mich.
Danke im Voraus.