Kraft auf Leiterschleife

Question

Aufgabe:

Eine Leiterschleife (der Widerstand des Leiters sei R) wird mit konstanter Geschwindigkeit v aus einem Magnetfeld gezogen.

a) Wie groß ist in der Leiterschleife induzierte Stromfluss?

b) Welche Kraft wird benötigt um die Leiterschleife wie beschrieben aus dem Magnetfeld zu ziehen?

c) Welche Leistung muss hierzu aufgebracht werden? Was passiert mit der umgesetzten Energie?

Problem/Ansatz:

Bei b) handelt es sich bestimmt um die Lorentz-Kraft. Und wie berechne ich Teilaufgaben a) und c), es sind wieder keine Zahlenwerte, nur Formel bzw. Zusammenhänge angeben? Danke und viele Grüße

Answer 1

Hallo,

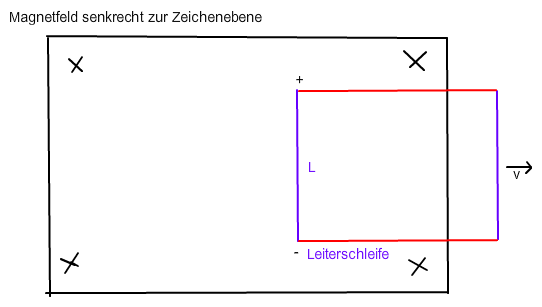
Wenn man eine rechteckige (#) Leiterschleife wie im Bild hat:

Die roten Leiterstücke haben keine Einfluss auf die Induktionsspannung, da sie während der Bewegung die magnetischen Feldlinien nicht schneiden.

Solange sich die gesamte Leiterschleife im Magnetfeld befindet, heben sich die Induktionsspannungen zwischen den Enden der blauen Leiterstücke auf.

Man hat also eine Induktionsspannung zwischen den Enden des linken blauen Leiters, wenn die Schleife wie im Bild liegt.

a)  Beim einem Leiter kennst du die Formel   U_ind  = B · L · v   →  I = U/R = B·L·v / R

b)  ja, das ist dann Lorentzkraft:  F_L = I · L · B , die nach dem Lenz'schen Gesetz gegen die Bewegungsrichtung gerichtet ist und deshalb die Bewegung bremst.

c)  Leistung P = F · s / t  = F · v  = I · L · B · v

----------

(#)  Allgemein kann man nur die Formeln  U_ind = - dΦ/dt   und  F_L = Q · \(\vec{v}\) x \(\vec{B}\)  benutzen.

Gruß Wolfgang

Comments

Vielen herzlichen Dank!

---

immer wieder gern :-)

Answer 2

Hallo

 1. beim rein oder Rauziehen ändert sich die Fläche, durch die B tritt nimm an die Schleife hat die Form  Rechteck a*b

U=B*A', I=U/R dadurch entsteht ein gegen B gerichtetes Feld, aber du hattest auch schon mal die Leiterschleife als DiPol? oder Kraft auf stromdurchflossenen Leiter , zeichne!

Leistung =Kraft*Weg/Zeit= Kraft *Geschwindigkeit,

der Draht wird warm!

Gruß lul

PS. es scheint du stellst hier alle deine HA ein ohne den geringsten Versuch selbst wenigstens Teile zu lösen?

Comments

Doch, das sollten Sie doch bei anderen Aufgaben sehen, dass ich die löse oder zumindest versuche Lösungsansätze zu machen, und da wo ich gar nicht weiterkomme, frage ich dann hier nach. Außerdem ist es öfters so, dass die Antworten erst einige Tage später kommen, so dass ich die Lösungen eher nicht mehr brauche, außer zum Verständnis der ganzen Thematik...