Gedämpfte Schwingungen Ein gedämpfter Feder‐Masse‐Schwinger

Question

Hallo habe Probleme bei dieser Aufgabe:

Ein gedämpfter Feder‐Masse‐Schwinger (Federkonstante D= 20 N/m, geschwindigkeitsproportionale Dämpfung)
wird zum Zeitpunkt t=0s um 20 cm ausgelenkt und losgelassen. Die Kreisfrequenz der Schwingung beträgt omega_d= 1,516
1/s. Die Amplitude des Schwingers hat nach zwei Schwingungsperioden um 40 % abgenommen.

Wie groß ist die noch vorhandene Schwingungsenergie nach 5 Schwingungsperioden?

wollte es mit dieser Formel machen, aber es klappt nicht:

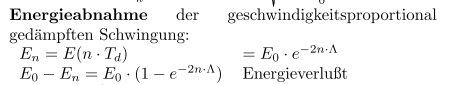
$$ \begin{array}{l}{\text { 3 a) } \Lambda=0,255} \\ {\text { 3 b) } m=8,7 \mathrm{kg}} \\ {\text { 3 c) } W=0,031 \mathrm{J}} \\ {\text { 3 d) } \mathrm{s}=0,14 \mathrm{m}}\end{array} $$

Aufgabe a b habe ich gelöst, komme bei c) nicht weiter

Answer 1

Hallo,

Wie groß ist die noch vorhandene Schwingungsenergie nach 5 Schwingungsperioden?

E₀ = 1/2 · 20 N/m · (0,2 m)² =  0,4 J    (elastische Energie der Feder in t=0)

Energie E_n (nach n Schwingungen)  =  E₀ · e^-2n·Λ

Nach n=5 Schwingungen also:   E₅  =  0,4 J · e^-2·5·0,255  ≈  0.0312 J 

Gruß Wolfgang

Comments

super vielen Dank,

hatte ich ja fast richtig :)