Relativistische Geschwindigkeitsaddition

Question

Aufgabe:

a)Zwei Elektronenstrahlkanonen senden in entgegengesetzter Richtung Elektronen der Geschwindigkeit 2,5*10^8 m/s aus. Wie groß ist die Geschwindigkeit des einen Elektronenstrahls, von einem Elektron des anderen Strahls aus beobachtet? (wenn dies möglich wäre)

b) Ein Elektron mit bewegt sich mit der Geschwindigkeit v=0,3c auf ein Photon (mit v=c, entgegengesetzte Richtung) zu. Welche Geschwindigkeit hat das Photon aus der Sicht des Inertialsystems Elektron?

Problem/Ansatz:

In beiden Fällen wird folgende Gleichung verwendet:

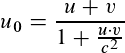
Hierbei ist c die Lichtgeschwindigkeit, u₀ ist die Geschwindigkeit in einem System S₀ (welches sich bewegt).

u ist die Geschwindigkeit im System S und v die Relativgeschwindigkeit zwischen S₀ und S.

zu a) 
2,5*10⁸  ist gleich 0,8333c 
Ich setzte in obige Gleichung für u und v jeweils 0,8333 ein und es kommt für u₀  das Ergebnis 0,983c raus.

Ist das Richtig? Wenn ja wie genau kann ich das Ergebnis interpretieren? Hier ist doch u₀ (also 0,983c) die Geschwindigkeit der einen Elektronen beobachtet aus der Sicht der anderen Elektronen.

zu b)

Gleiche Gleichung wird verwendet nur dass hier einmal für u 0,3c eingesetzt und für v=0,7c ? 
Das kommt mir hier falsch vor und ich weiß nicht wirklich weiter.

Allgemein fehlt mir etwas Verständnis für die Gleichung. Was genau ist mit der Relativgeschwindigkeit zwischen S₀ und S gemeint? Ist die "Vorstellung", dass S₀ ein bewegtes System ist und S ein stehendes richtig? 

Vielen Dank für Hilfe!!!

Answer 1

Hallo

a) ist richtig, wenigstens die Formel , Zahlen hab ich nicht nachgerechnet.

b) ist ne Art Fangfrage; überleg was die Rel.Th über c in verschiedenen Bezugssystemen sagt!

Gruß lul

Comments

Ahh, zu b): c ist maximal und wird nicht größer, (sieht man auch wenn man die Werte in die Formel einsetzt) 
Richtig? 

---

Was genau ist mit Relativgeschwindigkeit gemeint?

Vielen Dank für Ihre Hilfe!

Dieses ganze Inertialsystemzeugs ist wirklich verwirrend

---

"Im Bezugssystem S(t;x) fliegt ein Teilchen A mit der Geschwindigkeit v = 0,6c geradlinig auf das in S ruhende Teilchen B zu. Beide Teilchen haben in ihrem jeweiligen Ruhesystem die gleiche Ruhemasse m₀.

-Im Schwerpunkt System S' bewegen sich die Teilchen mit gleichen Geschwindigkeitsbeträgen direkt aufeinander zu.

- aus Sicht eines Beobachters X, der relativ zum Teilchen B im System S ruht, bewegt sich S' relativ zum Beobachter X mit der Geschwindigkeit v' und Teilchen A hat relativ zu S' den Geschwindigkeitsbetrag v.

Mit welchem Geschwindigkeitsbetrag v bewegt sich A relativ zum Inertialsystem S?"

Können Sie mir dort ähnlich wie bei Aufgabe b) einen Ansatz / eine Idee geben? :)

---

 eigentlich solltest du wirklich in b nichts rechnen, sondern wissen die Lichtgeschwindigkeit in Vakuum  ist in ALLEN Inertialsystemen gleich groß nämlich c .

Relativgeschwindigkeit  immer Relativ zu einem gegebenen A: wenn du im Auto mit 59km/h fährst, und dich as Bezugssystem nimmst ist deine Geschwindigkeit 0, di der Bäume am Straßenrand -50lm/h, ein entgegenkommendes Auto, das gegenüber dem Straßenrand mit 100km/h fährt hat dir gegegenüger, wenn es dir entgegenfährt die Geschwindigkeit -150km/h, wenn es in deiner Richtung fährt 50km/h Relativgeschwindigkeit.

 in der Rel-Th werden aber Geschwindigkeiten nicht so addiert sondern nach deiner Formel.

 für die andere Frage hast du ja nen neuen thread aufgemacht. Kennst du Minkowski Diagramme? darin kann man alles was unanschaulich scheint besser sehen und veranschaulichen.

Gruß

---

Ja ich dachte es sei übersichtlicher in einem neuen Thread.

Habe schon diesen Diagrammen gehört, aber wir haben sowas noch nicht besprochen.

Physik ist die letzten Wochen ausgefallen und wir kriegen nur EVA Aufgaben und dann besprechen in Einzelstunden dann mal die Lösungen. Ich hoffe mal wir besprechen sowas im Kurs, ansonsten schaue ich mal bei leifiphysik nach.

Vielen Dank für ihre Ausführungen!