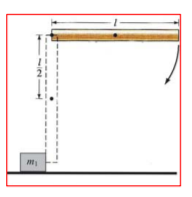
Eine drehbare Stange der Masse ms 0,3 kg und Länge 1 m wird aus der horizontalen Lage in die Vertikale fallen gelassen und stößt dort elastisch mit ihrem freien Ende auf die ruhende Masse m1 = 1kg.
Lösung:
Es gilt der Energieerhaltungssatz: $$\quad m _ { s } g \frac { l } { 2 } = \frac { 1 } { 2 } J _ { s } \omega ^ { 2 }$$
Massenträgheitsmoment der Stange: $$J _ { s } = \frac { 1 } { 12 } m _ { S } l ^ { 2 } + m _ { S } \left( \frac { l } { 2 } \right) ^ { 2 } = \frac { 1 } { 3 } m _ { S } l ^ { 2 } = 0,1 \mathrm { kg } m ^ { 2 }$$
Es folgt: $$\quad \quad m _ { s } g \frac { l } { 2 } = \frac { 1 } { 2 } \left( \frac { 1 } { 3 } m _ { s } l ^ { 2 } \right) \omega _ { 0 } ^ { 2 }$$
Lösung: $$\quad \omega _ { 0 } = \sqrt { \frac { 3 g } { l } } = \sqrt { \frac { 3 \cdot 10 m s ^ { - 2 } } { 1 m } } = 5,477 s ^ { - 1 }$$
Wieso ist beii der Lageenergie l/2? Die Höhe ist doch gleich der Länge der Stange.
Wieso wird beim Trägheitsmoment die Formel (durch die mitte genommen) Die Stange ist doch am Ende gelagert.
Dünner Stab \( J = ml^2 / 12 \) (quer durch die Mitte)
Dünner Stab \( J = ml^2 / 3 \) (Rotationsachse am Ende)
Warum nehmen Sie den Steineranteil?
Steiner \( J = J_{Schwerpunkt} + m·s^2 \)