Hallo,
zeichne Dir eine Zeit-Weg-Diagramm. Also ein Diagramm, wo auf der Horizontalen die Zeit und auf der Vertikalen der Ort aufgetragen ist. Die Bewegungen der beiden Tiere können dann als Funktion \(s(t)\) angegeben werden:
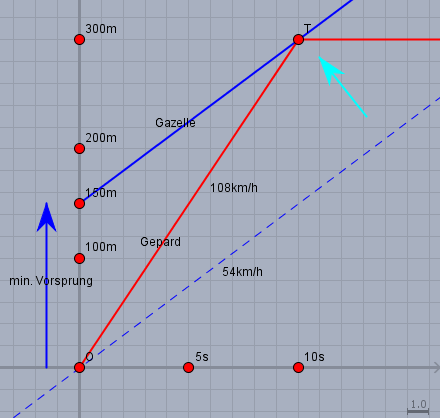
Die Bewegung des Gepards ist der rote Graph. Er soll bei \(s=0\) starten und läuft mit \(108 \text{km/h}\). D.h. mit wachsender Zeit wächst auch der Weg schnell an. Die Funktion des Gepards \(s_{Ge}\) ist:
$$s_{Ge} = 108 \frac{\text{km}}{\text{h}} \cdot t$$
Das gilt aber nur für den Zeitraum \(0 \le t \le 10\text{s}\). Danach nehmen wir mal an, dass er vor Erschöpfung einfach stehen bleibt. Beschleunigungen jeder Art werden hier nicht berücksichtigt. Nach diesen \(10\text{s}\) befindet sich der Gepard bei \(s_{Ge}(t=10\text{s})\) bzw. am Punkt \(T\) (s. Diagramm):
$$s_{Ge}(t = 10\text{s}) = 108 \frac{\text{km}}{\text{h}} \cdot 10\text{s} = 108 \frac{1000 \text{m}}{3600 \text{s}} \cdot 10\text{s} = 30 \frac{\text{m}}{\text{s}} \cdot 10\text{s} = 300 \text{m}$$
Würde die Gazelle zusammen mit dem Geparden bei \(s=0\) starten, so wäre ihr Weg der blau gestrichelte. Damit der Gepard sie nicht erwischt, muss man den Graphen parallel so weit verschieben (hellblauer Pfeil), dass die Gazelle vor dem Geparden bleibt, also der blaue Graph (Weg der Gazelle) muss immer höher sein, als der rote (Weg des Geparden). Der Weg \(s_{Ga}\) der Gazelle ist $$s_{Ga} = s_0 + 54 \frac{\text{km}}{\text{h}} \cdot t$$
Wobei \(s_0\) der minimal notwendige Vorsprung ist. Es ist ersichtlich, dass nach \(10\text{s}\) der 'kritische Punkt' erreicht ist - also muss sein: $$s_{Ga}(t= 10 \text{s}) \ge s_{Ge}(t = 10\text{s}) = 300 \text{m}$$ Einsetzen der Funktion der Gazelle gibt den notwendigen Vorsprung: $$\begin{aligned}s_0 + 54 \frac{\text{km}}{\text{h}} \cdot 10\text{s} &\ge 300 \text{m} \\ s_0 + 54 \frac{1000\text{m}}{3600\text{s}} \cdot 10\text{s}&\ge300 \text{m} \\ s_0 + 15 \frac{\text{m}}{\text{s}} \cdot 10\text{s}&\ge300 \text{m} \\ s_0 &\ge300 \text{m} - 150 \text{m} = 150 \text{m} \end{aligned}$$
Gruß Werner