Hallo,
du hast ja schon eine Skizze, zeichne/denke dir zur Veranschaulichung eine Linie, die durch das Pendel, wenn es ausgelenkt ist und durch senkrecht zu dem Pendel ist, wenn es nicht ausgelenkt ist.
So wie hier:
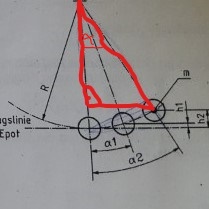
Die Hypothenuse des rechtwinkliges Dreiecks ist der Radius des Pendels bei dir R=0,8m
und die Ankathete von Alpha ist R-h
Daraus ergibt sich die Formel:
$$cos(\alpha)=\frac{R-h}{R}\\cos(\alpha)\cdot R=R-h\\cos(\alpha)\cdot R-R=-h\\h=-cos(\alpha)\cdot R+R$$
Das setzte du jetzt in die Formel für die potentielle Energie ein.
$${E}_{pot}=m\cdot g\cdot h\\{E}_{pot}=m\cdot h\cdot (-cos(\alpha)\cdot R+R)$$
Setzt dort deine Werte ein und verstehe die Gleichung.
Bei b kann mit sich den Energieerhaltungssatz zu Nutze machen.
$${E}_{kin}={E}_{pot}\\\frac{m}{2}\cdot v^2=m\cdot g\cdot (-cos(\alpha)\cdot R+R)\\v=\sqrt{2g\cdot(-cos(\alpha)\cdot R+R)}$$
Versuche auch die Gleichung zu verstehen. Wenn du zu Zwischenschritten fragen hast, dann frag in Kommentaren.
c) Hierzu muss man Epot2 als Energie bei der Auslenkung α2 sehen und Epot1 und Ekin1 bei bei α1
Hier gilt dann:
$${E}_{pot2}={E}_{pot1}+{E}_{kin1}\\m\cdot g\cdot {h}_{2}=m\cdot g\cdot {h}_{1}+\frac{m}{2}\cdot v^2$$
Für h können wir die oben hergeleitete Formel verwenden, jeweils mit den beiden verschiedenen Winkeln. h2 ist natürlich die Höhe bei 30° und h1 die Höhe bei 15°, zumindest in der Formel die ich jetzt habe. Ich kann das aus deinem Zettel nicht richtig ablesen, welche Höhe zu welchem Winkel gehört. Sonst musst das dementsprechend anpassen.
$$g\cdot (-cos({\alpha}_{2})\cdot R+R)=g\cdot (-cos(\alpha)\cdot R+R)+\frac{v^2}{2}\\v=\sqrt{2\cdot g\cdot R\cdot(cos({\alpha}_{\boldsymbol{1}})-cos({\alpha}_{\boldsymbol{2}}))}$$
Mit der Gleichung kannst du die Aufgabe lösen und wieder: Verstehe die Umformungen.
Mit freundlichen Grüßen
Smitty