Stromstärke bei zwei Spannungsversorgungen berechnen (LGS 2 unbekannte)

Question

Zwei Stromquellen arbeiten entsprechend nebenstehender Schaltung auf die drei Widerstände R1 R2 und R3.

Wie groß sind die Ströme in den drei Widerständen und die Spannung U3 am Widerstand R3?
Diese Aufgabe soll durch Gleichungssystemen gelöst werden, andere Lösungen sind aber auch gerne gesehen! :)

Mein Problem hierbei liegt daran, das ich die Gleichungen nicht richtig aufgestellt bekomme denke ich :\

hier mein Ansatz:

I.$$U_1=(R_1+R_3)I1-(R2+R3)I2$$

und bei der zweiten Gleichung habe ich leider keine Ahnung wie sie aussehen soll... :\ ich würde nur vermuten das ich hier die Spannung gleich 0 Setze weil man ja das Kirchhoff'sche Gesetz anwenden kann (die summe aller ströme in einem geschlossenen Stromkreis ist gleich 0) aber keine Ahnung was dann auf die andere Seite kommt... :\

Answer 1

I1+I2 -I3 =0

Masche 1 : R1I1 +R3I3 - Iu1R1 = 0

Masche 2 : R2I2 +R3I3 - U2 = 0

Answer 2

du willst also die Ströme über die Kirchhoffschen Gesetze berechnen?

Du kannst alternativ das Problem über den Überlagerungssatz lösen

 

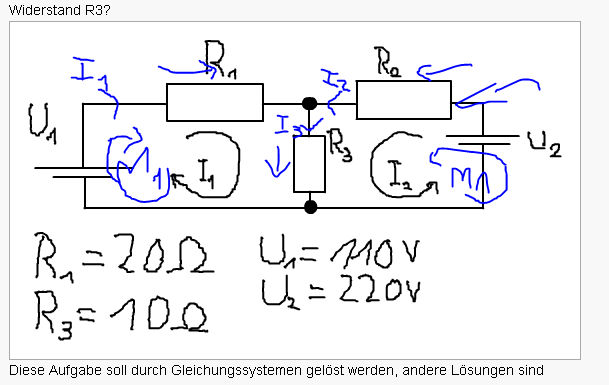
Deine Schaltung hat zwei Maschen. Die Linke nenne ich M1 und die Rechte M2

 

Maschenumlauf M1 (starte oben linke Ecke und gehe rechts rum)

 

I1*R1 + I3*R3 - U1 = 0

 

Maschenumlauf M2 (starte rechte obere Ecke und gehe links rum)

 

I2 * R2 + I3*R3 - U2 = 0

 

Deine beiden Gleichungen für die Matrixdarstellung (Gaußeralgorithmus)

 

I1*R1 + I2*0      + I3*R3         = U1

I1*0    + I2 * R2 + I3*R3        =  U2

 

 

(die summe aller ströme in einem geschlossenen Stromkreis ist gleich 0)

Das ist Falsch.

1. Kirchhoffsche Regel: Die Summe der Ströme an einem Knoten ist 0

2. Kirchhoffsche Regel: Die Summe der Spannungen in einem Maschenumlauf ist 0

Comments

Das mit dem Überlagerungssatz schein auf jeden Fall eine gute Idee zu sein ;) habe auch soweit nachvollziehen können wie die Gleichungen zustande kommen, aber danach habe ich ja noch kein Gleichungssystem, ich habe ja noch die unbekannten R2 und I3 wären dann ja 4 insgesamt.

R2 und I3 kann ich doch so ohne weiteres nicht berechnen oder?

---

Du hast Recht, ich habe noch eine dritte Gleichung vergessen.

Das ist nämlich nur die erste Kirchhoffsche Regel am oberen Knotenpunkt (wo I1, I2 aufeinandertreffen)

 

i)   I1 + I2 - I3   = 0

ii)  I1*R1 + I2*0      + I3*R3         = U1

iii) I1*0    + I2 * R2 + I3*R3        =  U2

 

Ich merke aber auch gerade, dass R2 gar nicht vorgegeben ist. Das ist jetzt etwas blöd.

 

(1 1 - 1      | 0  )

(R1 0 R3  | U1)

(0 R2 R3 | U2 )

 

Das ist die Koeffizientenmatrix, damit kann man I1, I2, I3 ausrechnen.

---

Vielen dank! :)

nur leider kann man da ohne R2 nicht viel machen oder? :\