Hallo,
zunächst die Antworten auf die im Kommentar gestellten Fragen:
Was bedeutet Z ?: Z ist eine beliebige Impedanz
Warum ist I4 wie eine Spannungsquelle und nicht wie eine Stromquelle gezeichnet ? : Den Wert eine Spannungsquelle kann man mit U angeben. Man kann aber auch den Wert einer Spannungsquelle als Produkt einer beliebigen Impedanz Z multipliziert mit einem beliebigen Strom I angeben, denn das Produkt aus Impedanz mal Strom ist ja eine Spannung. In der Aufgabe hat also die Spannungsquelle den Wert Z*I4 .
Nun zur lösung der Aufgabe:
In dem Netzwerk fließen 8 verschiedene Ströme. Folglich werden 8 Gleichungen benötigt, die voneinander linear unabhängig sind.
Z.B. 5 Knotenpunkt und 3 Maschengleichungen wie im Bild 1 und Bild 2 angegeben.
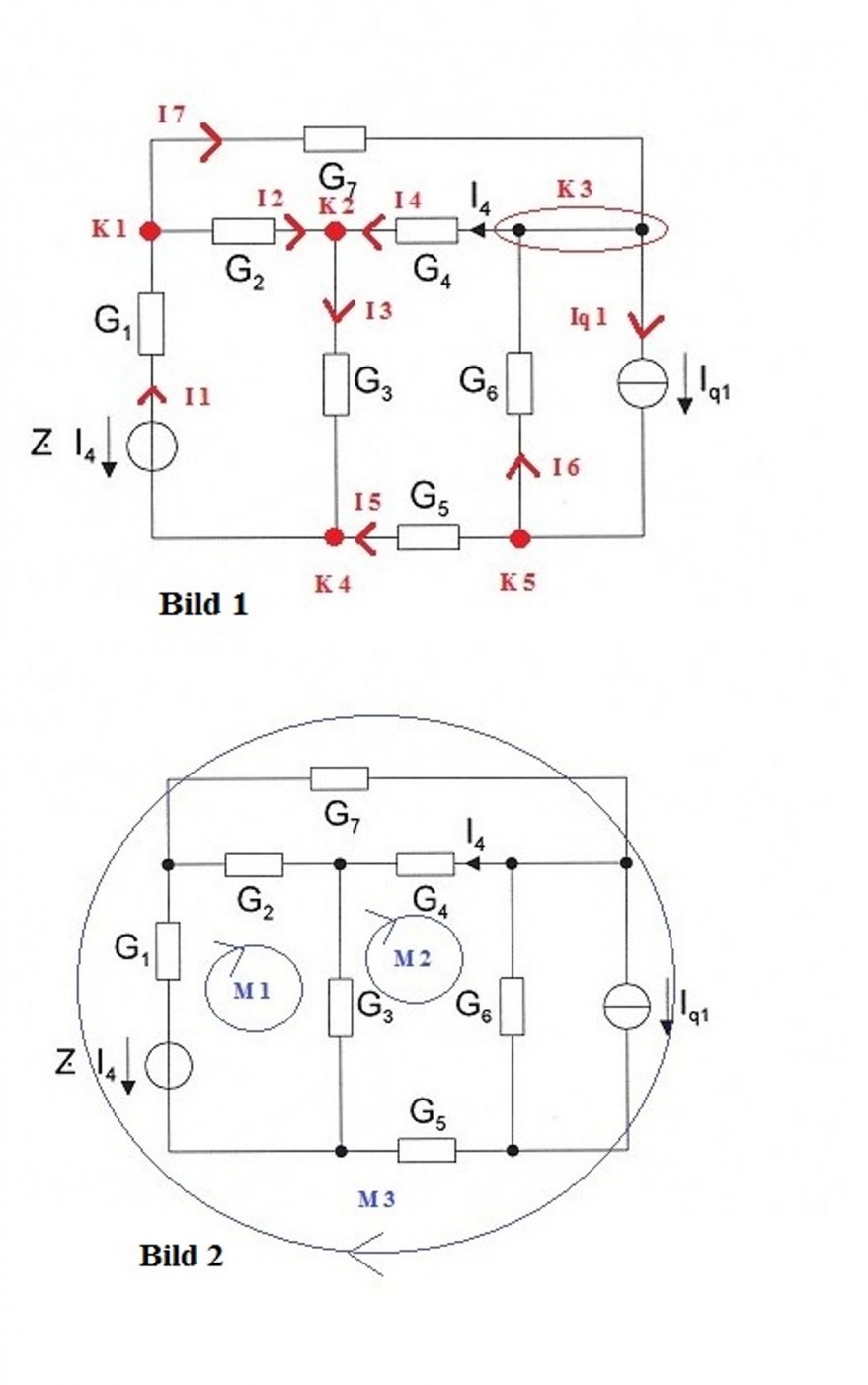
Die Gleichungen lauten:
K1: \(I_{1} - I_{2} - I_{7} = 0\)
K2: \(I_{2} + I_{4} - I_{3} = 0\)
K3: \(I_{7} + I_{6} - I_{4} - I_{q1} = 0\)
K4: \(I_{3} + I_{5} - I_{1} = 0\)
K5: \(I_{q1} - I_{5} - I_{6} =0\)
M1: \(\frac{I_{1}}{G_{1}} + \frac{I_{2}}{G_{2}} + \frac{I_{3}}{G_{3}} - Z*I_{4} = 0\)
M2: \(\frac{I_{5}}{G_{5}} - \frac{I_{3}}{G_{3}} - \frac{I_{4}}{G_{4}} - \frac{I_{6}}{G_{6}} = 0\)
M3: \(\frac{I_{1}}{G_{1}} + \frac{I_{7}}{G_{7}} - \frac{I_{6}}{G_{6}} + \frac{I_{5}}{G_{5}} - Z*I_{4} = 0\)
Damit ist das Gleichungssystem aufgestellt und kann mit den bekannten Methoden gelöst werden
Gruß von hightech