Hallo Hellin,
mache Dir bitte eine Zeichnung. Die könnte etwa so aussehen:
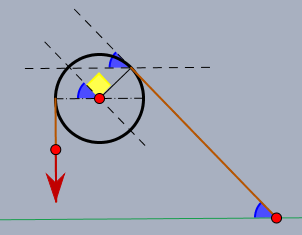
alle blauen Winkel sind gleich (Stufenwinkel an Parallelen) und haben den Wert \(\alpha\). Der gelbe Winkel ist ein rechter. Dann ist offensichtlich: $$\varphi = \alpha + \frac{\pi}{2}$$ Die Gewichtskraft von \(m_2\) sei \(G_2=m_2 \cdot g\). Die Seilkraft im rechten Teil sei \(S\). Die Masse \(m_1\) mit dem Gewicht \(g_1=m_1 \cdot g\) drückt mit der Kraft \(G_1 \cdot \cos \alpha \) auf die schiefe Ebene und zieht mit \(G_1 \cdot \sin \alpha\) am Seil (mach' Dir selber mal 'ne Zeichnung dazu). Zusammen mit der Haftreibung und der Euler-Eytelwein-Formel erhält man $$m_2 \cdot g \le S \cdot e^{\mu_{H2} (\alpha + \pi/2)}$$ und $$S \le G_1 \cdot \sin \alpha + \mu_{H1} \cdot G_1 \cdot \cos \alpha = m_1 \cdot g \cdot (\sin \alpha + \mu_{H1} \cdot \cos \alpha )$$ Zusammengefasst und nach \(m_1\) isoliert: $$m_1 \ge \frac{m_2}{(\sin \alpha + \mu_{H1} \cdot \cos \alpha ) \cdot e^{\mu_{H2} (\alpha + \pi/2)}} $$