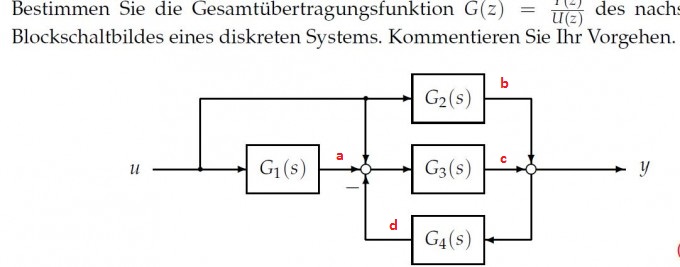
Hallo,
ich hab das schon länger nicht mehr gemacht, aber mMn geht das so. Man setzt hier an den Ausgängen der einzelnen Systeme Variablen, schreibt sie an und setzt sie ineinander ein, bis man auf ein b und c kommt, das nur mehr von y und u abhängig ist. Man sieht sofort, dass \( a = uG_1 \) und \( b = uG_2 \).
$$ d = (b+c)G_4 = bG_4 + cG_4 = uG_2G_4 + cG_4 $$
Das d und a kann man nun in c einsetzen.
$$ c = (a-d+u)G_3 = aG_3 -dG_3 +uG_3 = uG_1G_3 - (uG_2G_4 + cG_4)G_3 + uG_3 = uG_1G_3 - uG_2G_3G_4+cG_3G_4 + uG_3$$
$$ \Leftrightarrow c - cG_3G_4 = u(G_1G_3-G_2G_3G_4+G_3) $$
$$ c(1-G_3G_4) = u(G_1G_3-G_2G_3G_4+G_3) \Leftrightarrow c = \left( \frac{G_1G_3-G_2G_3G_4+G_3}{1-G_3G_4} \right) u $$
Nun schaut man sich das y an:
$$ y = b + c = uG_2 + \left( \frac{G_1G_3-G_2G_3G_4+G_3}{1-G_3G_4} \right) u = u \left(G_2 + \frac{G_1G_3-G_2G_3G_4+G_3}{1-G_3G_4} \right) = u \left( \frac{G_2 -G_2G_3G_4 + G_1G_3-G_2G_3G_4+G_3}{1-G_3G_4} \right) $$
Nun formt man auf die Form \( \frac{y}{u} \) um und hat damit die Übertragungsfunktion:
$$ G = \frac{y}{u} = \frac{G_2 -G_2G_3G_4 + G_1G_3-G_2G_3G_4+G_3}{1-G_3G_4} $$