Zu a )
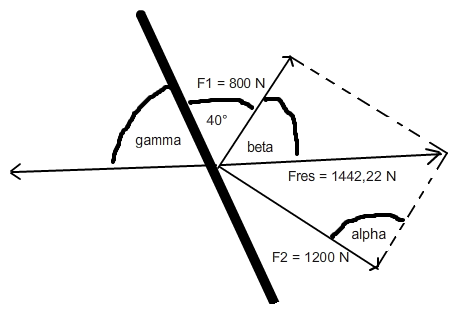
Die resultierende Kraft FRes, die sich aus zwei in unterschiedlicher Richtung wirkenden Kräfte ergibt, ist gleich der Länge der Diagonalen des Parallelogramms, welches aus den zwei gegebenen Kräften gebildet wird (Kräfteparallelogramm).
Diese Diagonale ist vorliegend besonders einfach zu berechnen, da die beiden Kräfte im rechten Winkel zueinander stehen und das durch sie gebildete Parallelogramm daher ein Rechteck ist. Die Länge der Diagonalen d eines Rechtecks mit den Seiten a und b aber ist (gemäß Pythagoras):
d = √ ( a 2 + b 2 )
sodass sich vorliegend ergibt:
FRes = √ ( F1 2 + F2 2 ) = √ ( 800 2 + 1200 2 ) = √ 2080000 = 1442,22 N (gerundet)
[ Anmerkung: Im allgemeinen Fall ist die Länge der Diagonalen des Kräfteparallelogrammes mit Hilfe des Kosinussatzes
d 2 = a 2 + b 2 - 2 * a * b * cos ( alpha )
zu berechnen, wobei der Winkel alpha derjenige Winkel des Kräfteparallelogramms ist, der der zu berechnenden Diagonale gegenüberliegt.
Im vorliegenden Spezialfall (Kräfteparallelogramm ist ein Rechteck) ist der Winkel Alpha (wie alle Winkel eines Rechtecks) gleich 90 °. Wegen cos ( 90 ° ) = 0 entfällt der entsprechende Summand im Kosinussatz und es verbleibt der dem Satz des Pythagoras entsprechende Teil. ]
Zu b )
Das Spannseil muss der aus den Kräften F1 und F2 resultierenden Kraft entgegenwirken, um diese zu kompensieren. Für seinen Richtungswinkel gamma (bezogen auf die Freileitung, siehe Skizze) muss also gelten:
gamma = 180 - beta - 40 °
wobei beta der Winkel zwischen der resultierenden Kraft FRes und der Kraft F1 ist. Für diesen Winkel gilt:
beta = arccos ( F1 / F Res ) = arccos ( 800 / 1442,22 ) = 56,31 °
sodass sich für den Winkel gamma ergibt:
gamma = 180 - 56,31 - 40 = 83,69 °