Hallo,
Der Gabelhaken wird sich so einpendeln, dass sich sein Schwerpunkt genau unter dem Aufhängepunkt \(A\) befindet. Um die Position des Schwerpunkts zu berechnen müssen die Positionen der einzelnen Schwerpunkte entsprechend gewichtet addiert werden.
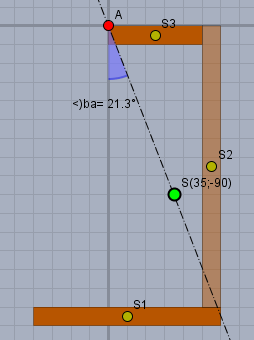
Da alle Balkenstücke gleichen Querschnitt haben, verhalten sich ihre Gewichte wie ihre Längen. Nummeriere ich die Balken von unten nach oben von 1 bis 3, so verhalten sich ihre Gewichte \(g_i\) wie
$$g_1 \div g_2 \div g_3 = 10 \div 15 \div 5$$ mit der Summe aller Gewichtungen von \(w=10 + 15 +5 = 30\). Demnach ist der Schwerpunkt \(s\) (alle Längen in \(\text{cm}\))
$$s = \sum \frac{w_i}{w} s_i = \frac{10}{30} \begin{pmatrix} 10\\ -155\end{pmatrix} + \frac{15}{30} \begin{pmatrix} 55\\ -75 \end{pmatrix} + \frac{5}{30} \begin{pmatrix} 25\\ -5 \end{pmatrix}= \begin{pmatrix} 35\\ -90\end{pmatrix} $$
Das Koordinatensystem habe ich zur Definition der Schwerpunktpositionen in den Aufhängepunkt gelegt. Und der Winkel \(\delta\), um den sich der Gabelhaken eindrehen wird, liegt dann bei
$$\delta = \arctan{\frac{35}{90}} \approx 21,25°$$
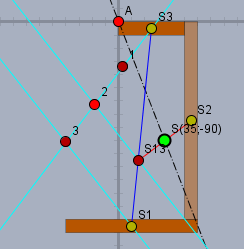
Als Goody noch eine graphische Konstruktion des Schwerpunkts. Die Gewichte \(g_1\) und \(g_3\) verhalten sich wie 2 zu 1. Folglich liegt der gemeinsame Schwerpunkt der Balken 1 und 3 in einem Punkt \(S_{13}\) der die Strecke \(\overline{S_1S_3}\) im Verhältnis \(1 \div 2\) teilt. Die Summe der Gewichte der Balken 1 und 3 ist identisch zum Gewicht von Balken 3. Folglich liegt der Gesamtschwerpunkt genau in der Mitte zwischen \(S_{13}\) und \(S_2\).
Gruß Werner