Bei sowas solltest Du Dir immer eine Skizze machen. Etwa so:
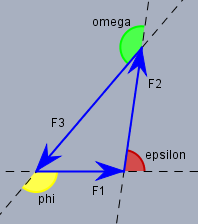
Dann sieht man, dass die gesuchten WInkel die Nebenwinkel der Innenwinkel eines Dreiecks sind, das von den drei Kräften aufgespannt wird. Nach Cosinussatz gilt z.B. für \(\epsilon\):
$$\cos( \pi- \epsilon ) = \frac{F^2_1 + F^2_2 - F^2_3}{2 \cdot F_1 \cdot F_2} \quad \Rightarrow \space \epsilon\approx 83,55°$$
Die beiden anderen Winkel lassen sich genauso berechnen. Tipp: die Winkelsumme ist hier \(\epsilon + \omega + \varphi=360°=2\pi\).
Die Aufgabe ist übrigens nicht eindeutig gestellt. Es gibt noch eine zweite Lösung; ordne dazu die Kräfte genau spiegelverkehrt an.