Wurfbewegungen Physik berechnen

Question

Ich komme bei Nr.2 nicht weiter, kann mir jemand helfen? Vielen Dank 

Comments

Ich habe die Fragen zusammengeführt.

Eine Bitte an den Fragesteller:

BITTE NACHFRAGEN ZU BEREITS BESTEHENDEN FRAGEN IN DER FRAGE STELLEN UND KEINE NEUEN FRAGEN ERÖFFNEN!

Answer 1

h ( a ) = 100 m
h ( B ) = 0 m

Strecken
Von A nach unten
sA = freier Fall plus Anfangsgeschwindigkeit  * t
sA = 1/2 * g * t^2 + 10 * t

Von B nach oben
sB = Anfangsgeschwindigkeit * t ( nach oben ) minus freier Fall
sB = 10 * t  - 1/2 * g * t^2

sA + sB = 100
1/2 * g * t^2 + 10 * t  + 10 * t  - 1/2 * g * t^2 = 100
berechnet
20 * t = 100
t = 5 sec

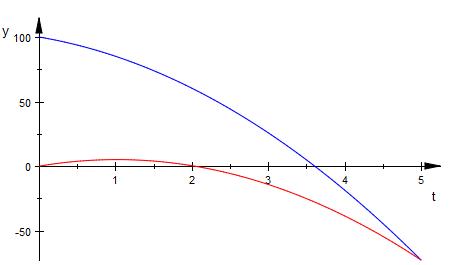
Der Treffpunkt befindet sich 72.63 Meter unterhalb von Punkt A

Comments

Danke sehr :-) & wie komme ich auf die 72,63m?

---

Du brauchst t = 5 sec nur in
sB ( t ) = 10 * t  - 1/2 * g * t²
einsetzen ( rote Kurve )
sB ( 5 ) = 10 * 5  - 1/2 * g * 5^2
sB ( 5 ) = -72.63 m

sA ( 5 ) = 1/2 * g * 5² + 10 * 5
sA ( 5 ) = 172.63 m

Dies wäre die zurückgelegte Weg nach unten
Da von 100 m begonnen wurde ergibt sich
100 - 172.63 m = -72.63 m
( blaue Kurve )

---

Vielen Dank :) & um die Zeit rauszufinden hätte ich die beiden Gleichungen auch gleichsetzen können, doch ich weiß nicht wie diese t's wegkürzen kann :S könntest du mir vielleicht zeigen, wie man diese Gleichung auflöst? Wäre super

---

Auf der rechten Seite hat du einen kleinen Fehler
Anstelle
v0 * t * 1/2 * g * t^2
muß es heißen
v0 * t  - 1/2 * g * t^2

- 1/2 * g * t^2 entfällt dann

Es bleibt übrig
100 - v0 * t = v0 * t
2 * v0 * t = 100
t = 5

---

Vielen vielen Dank es hat mir sehr geholfen und deine Antworten waren immer am besten. Du hast mir vieles erleichtert super vielen Dank :-)))

---

Ich habe noch eine kleine Frage der Schritt vor dem Ergebnis, wo kommt da die 2 her?

---

100 - v0 * t = v0 * t   | + v0 * t
100 = 2 * v0 * t
2 * v0 * t = 100
t = 5

---

Cool danke!!! :-)