hi
I. s = 1/2 atb²
II. a = v/tb
II. in I.
s = 1/2 (v/tb)tb²
s = 1/2 vtb
tb = 2s/v
tb = 2*4000/(120/3.6) = 240s
bremszeit: 240 sekunden. nach 4 minuten kommt der schnellzug zum stehen
in dieser zeit legt der güterzug s = vtb = (40/3.6)*240 ≈ 2667 meter zurück.
er hätte aber 3000 meter zurücklegen müssen, damit er nicht vom schnellzug gerammt wird.
bewegungsgleichung für den schnellzug: s(t) = vst + (1/2)at²
bewegungsgleichung für den güterzug: g(t) = vgt + 1000
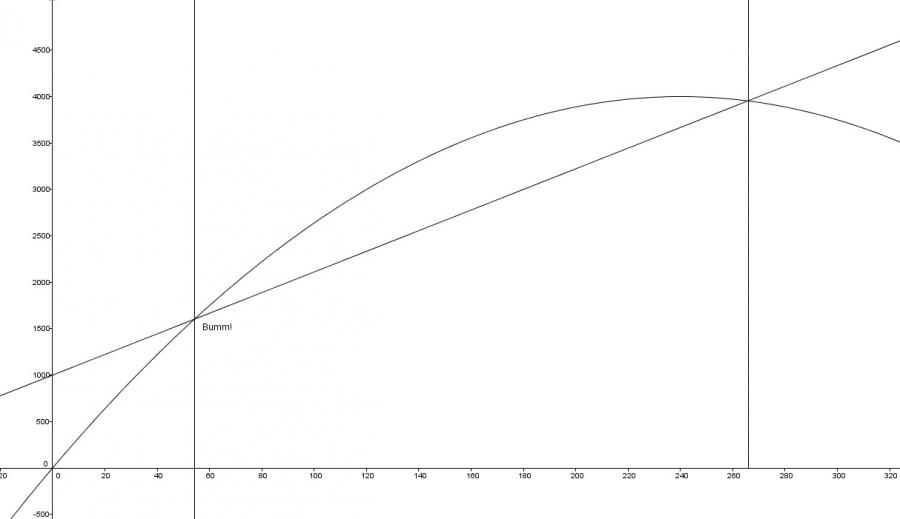
um den zeitpunkt des aufpralls zu berechnen, setzen wir
s(t) = g(t)
vst + (1/2)at² = vgt + 1000
t kommt quadratisch vor, das riecht verdächtig nach quadratischer gleichung.
vorbereitung für die pq formel:
vst + (1/2)at² - vgt - 1000 = 0
(1/2)at² + (vs-vg)t - 1000 = 0
t² + 2(vs-vg)t/a - 1000/a = 0 | a = (120/3.6)/240 = -5/36 m/s²
t² + 2((120-40)/3.6)t/(-5/36) - 1000/(-5/36) = 0
t² - 320t + 14400 = 0
t1,2 = 160 ± √(160²-14400)
t1 ≈ 265.8s
t2 ≈ 54.2s
rein intuitiv mochte man wohl im ersten teil der aufgabe meinen, der aufprall würde
kurz vor dem eigentlichen stillstand des schnellzuges stattfinden - aber -
weit gefehlt! es scheppert bereits bei t = 54.2 sekunden, am ort s = vg*t = 40/3.6 * 54.2 ≈ 1602 meter.
lg