Aufgabe:
Stimmt die Rechnung (Die lösung in der Aufgabenstellung muss nicht zwingend richtig sein!!)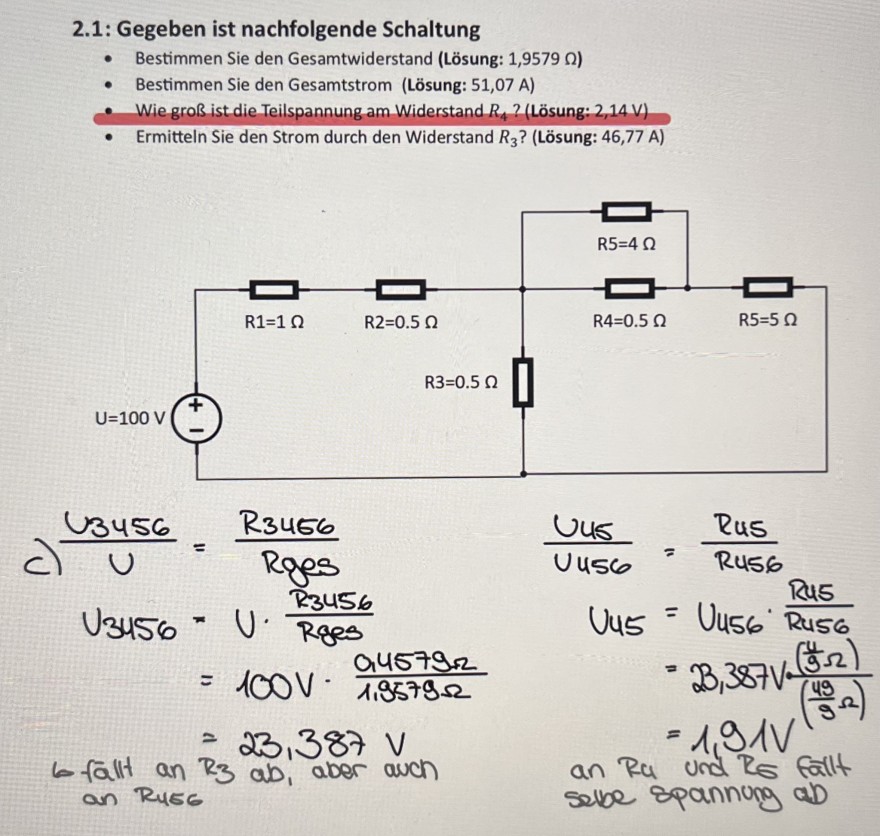
Text erkannt:
2.1: Gegeben ist nachfolgende Schaltung
- Bestimmen Sie den Gesamtwiderstand (Lösung: 1,9579 \( \Omega \) )
- Bestimmen Sie den Gesamtstrom (Lösung: 51,07 A)
- Wie groß ist die Teilspannung am Widerstand \( R_{4} \) ? (Lösung: 2,14 V)
- Ermitteln Sie den Strom durch den Widerstand \( R_{3} \) ? (Lösung: 46,77 A)
\( \begin{array}{l} \text { c) } \frac{U_{3456}}{U}=\frac{R_{3456}}{R_{\text {ges }}} \quad \frac{U_{45}}{V_{456}}=\frac{R_{45}}{R_{456}} \\ U_{3456}=V \cdot \frac{R_{3456}}{R g e s} \\ =100 \mathrm{~V} \cdot \frac{0,4579 \Omega}{1,9579 \Omega} \\ =23,387 \mathrm{~V} \\ U_{45}=U_{456} \cdot \frac{R_{45}}{R_{456}} \\ =23,387 \mathrm{~V} \cdot \frac{\left(\frac{4}{3} \Omega\right)}{\left(\frac{49}{9} \Omega\right)} \\ =1,91 \mathrm{~V} \end{array} \)
6 fallt an \( R_{3} \) ab, aber auch an R456
Und wenn ja, wieso wird erstmal die Spannung der einen Masche berechnet ?