Wie erklärt sich diese Anwendung der Formel zum Weg-Zeit-Gesetz?

Question

Aufgabe:

Durch eine Notbremsung wird ei Zug von einer konstanten Geschwindigkeit von 144 km/h in 20 Sekunden auf 72 km/h
gleichmäßig abgebremst. Dann prallt der Zug in die Erdmasse und kommt innerhalb von
0,2 s zum Stehen.

Ich frage mich Warum in der Formel untenstehend, (72-0/3,6*0,2)*0,2^2 steht,

denn meiner Logik nach müsste dort doch (72-0/3,6)*02^2 stehen.

da deltav= a*t und somit s= 1/2*a*t^2

Freue mich über jede Hilfe

Liebe Grüße Ortwin

\( \begin{aligned} s &=\frac{1}{2} \cdot\left(\frac{72-0}{3.6 \cdot 0.2} \cdot 0.2^{2}+\frac{144-72}{3.6 \cdot 20} \cdot 20^{2}\right) \mathrm{m} \\ &=202 \mathrm{~m} \end{aligned} \)

Text erkannt:

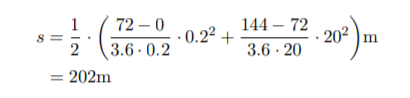
Text erkannt:

\( \begin{aligned} s &=\frac{1}{2} \cdot\left(\frac{72-0}{3.6 \cdot 0.2} \cdot 0.2^{2}+\frac{144-72}{3.6 \cdot 20} \cdot 20^{2}\right) \mathrm{m} \\ &=202 \mathrm{~m} \end{aligned} \)

Answer 1

Hallo Ortwin,

Die Formeln lauten doch :

s = 1/2 * a * t² und Δv = a * t → a = Δv / t, also ergibt sich, wenn du in die erste Gleichung Δv/t für a einsetzt:

s = 1/2 * (Δv/t) * t²

Deshalb werden die Brüche mit 0,2² und 20² multipliziert und im Nenner stehen die 0,2 und 20.

Es könnte natürlich noch gekürzt werden, so dass dann davon nur noch 0,2 und 20 übrig bleiben.

In Einheiten : (m/s) * s = m

denn meiner Logik nach müsste dort doch (72-0/3,6)*02² stehen.

Nach deiner Logik käme für den Weg, keine Längenmaßeinheit, nämlich "m" , sondern

(m/s) * s² = "m*s"

heraus.

Gruß

Enano