Hallo :-)
Aus deinen gegebenen Messdaten kann ich mittels linearer Regression mit geratener Ansatzfunktion \(F(s)=a\cdot \sqrt{s}+b\cdot e^s\) folgendes Näherungsergebnis erhalten:
$$F(s)\approx 0.884373\cdot \sqrt{s}+1.940122\cdot 10^{-5}\cdot e^s$$.
Skizze:
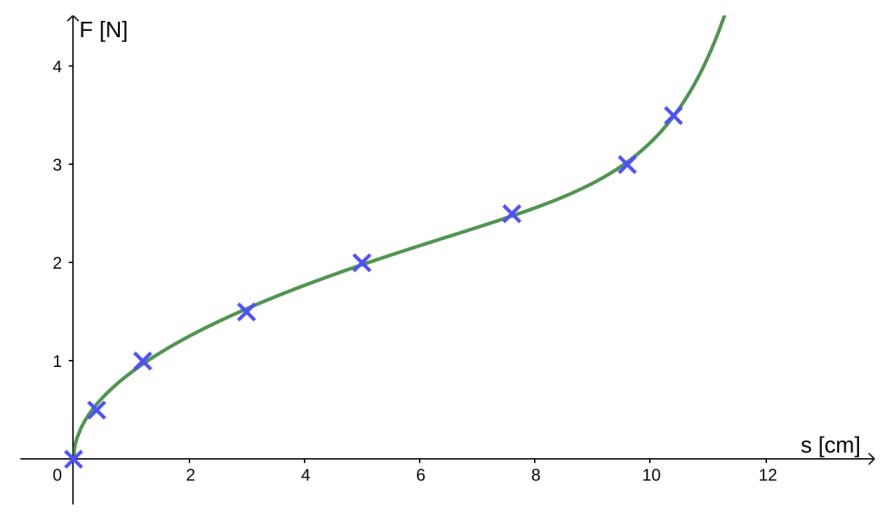Dann habe ich bei (1) zb für \(s=4\) schätzungsweise $$F(4)\approx 0.884373\cdot \sqrt{4}+1.940122\cdot 10^{-5}\cdot e^4\approx 1.77$$
Bei (2) kann man durch Ablesen erkennen, dass bei einer Kraft von \(1.2N\) etwa \(s=1.8cm\) Verlängerung zu erwarten ist. Du kannst auch direkt $$0.884373\cdot \sqrt{s}+1.940122\cdot 10^{-5}\cdot e^s=1.2$$ betrachten, was zb mit dem Newton-Verfahren zu folgendem Näherungsresultat führt: \(s\approx 1.837\).
Bedenke, dass meine Ansatzfunktion nicht physikalisch erklärbar ist, sondern ich habe sie emperisch ermittelt, weshalb hier die Einheiten nicht passend sind und ich hier nur mit den Zahlen gearbeitet habe.
2.) Ansatz: \(F=D\cdot \Delta l \quad \Leftrightarrow \quad \Delta l=\frac{F}{D}=\frac{12.5N}{2\frac{N}{cm}}=6.25cm\).
