Mit welchem Mindestradius sollte abgerundet werden?

Question

Aufgabe:

Mit welchem Mindestradius sollte der Übergang abgerundet werden, sodass Autos, die mit 90 km/h fahren, nicht von der Strasse abheben?

Problem/Ansatz:

Die Planung einer neuen Strasse umfasst ein gerades Streckenstück, das horizontal und flach ist, aber plötzlich in einen steilen Abhang mit einem Gefälle von 22 Grad übergeht.

Mit welchem Mindestradius sollte der Übergang abgerundet (als portion eines kreises betrachtet) werden, sodass Autos, die mit 90 km/h fahren, nicht von der Strasse abheben?

Hinweis: Der Übergang beginnt im Punkt X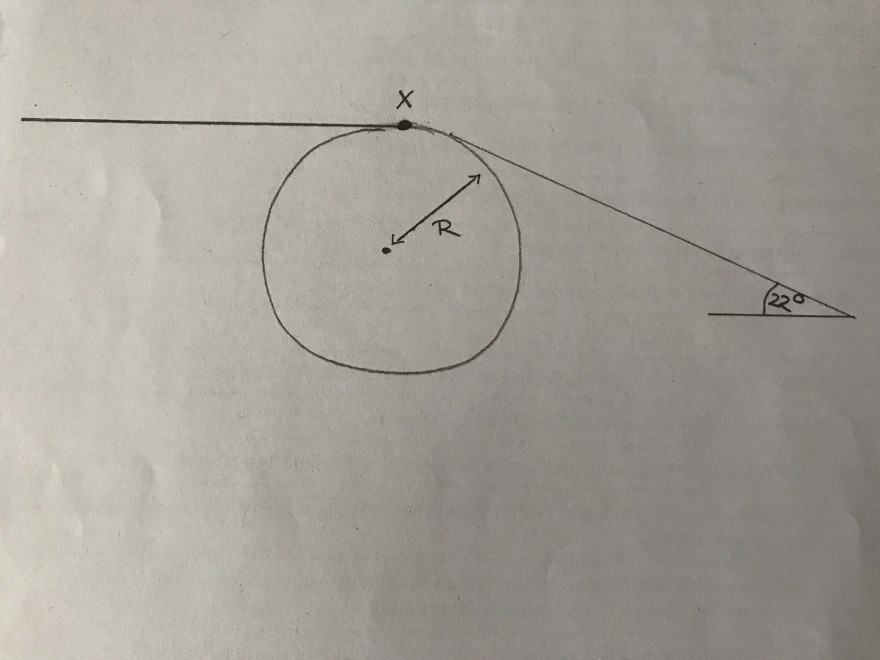

Text erkannt:

\( (3)= \)

Comments

 da muss noch die Haftreibungskraft angegeben sein, denn sie ist die einzige Kraft, die die nötige Zentripetalkraft ausübt, also Reibungskraft=Zentripetalkraft

---

Hat nichts mit Haftreibung zu tun.

Deine Antwort ist auch keine Antwort, sondern ein Kommentar.

Answer 1

Ich interpretiere so:

Ein Massepunkt mit einer Horizontalgeschwindigkeit von 25m/s geht in horizontalen Wurf über.

Die Wurfparabel kann mit $$p(x)=- \frac {g}{v^2} \cdot x^2$$

beschrieben werden.

Die Ableitung der Wurfparabel lautet $$p'(x)=- 2 \frac {g}{v^2} \cdot x$$

Der Winkel der abhängenden schiefen Ebene beträgt 22°, was einem Gefälle von 40% entspricht.

Es muss also die Stelle gesucht werden, an der die Parabel diese Steigung aufweist:

$$p'(x)=- 2 \frac {g}{v^2} \cdot x$$

$$p'(x)=-\frac{40}{100}$$

$$-\frac{40}{100}= -2 \frac {10}{25^2} \cdot x$$

$$\frac{20}{100}=\frac {10}{25^2} \cdot x$$

$$\frac{20\cdot 25^2}{1000}= x$$

Diese Stelle liegt 12,5m hinter dem "Absprung" und hat die Koordinaten B=(12,5|2,5)

Nun muss ein Kreis durch die Punkte Absprung(0|0) und B gelegt werden, dessen Mittelpunkt sich auf der y-Achse befindet.

Comments

Fortsetzung:

Der Mittelpunkt des Kreises liegt bei M=(0|-32,5) und hat daher einen Radius von R= 32,5 m

Sofern Interesse, erläutere ich noch gern, wie man dazu kommt.