Hallo Schwinge,
Es geht also darum die Kraft des Wassers, die es auf eine senkrecht stehende halbkreisförmige Fläche ausübt, zu berechnen. Ganz allgemein ist die Kraft \(F\) die Summe aller Einzelkräfte und da diese infinitisimal klein sind, wird es gleich ein Integral $$F = \int \text d F$$Diese \(\text d F\) sind im wesentlichen vom Wasserdruck abhängig. Also suchen wir uns eine Bereich, wo dieser Druck konstant ist.
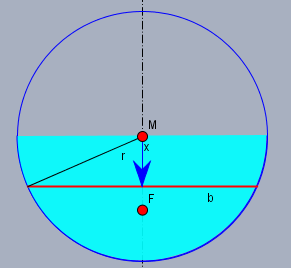
Das ist die rote Linie gleicher Tiefe in der Tiefe von \(x\). Die Kraft ist Druck \(p\) mal Fläche \(A\). Und die Fläche ist der rote Strich mit der infinitisimal kleinen Höhe \(\text d x\) und der Breite \(b\). Also $$\text d F = p \cdot A = p \cdot b \, \text dx$$
Der Wasserdruck \(p\) ist natürlich von der Tiefe \(x\) abhängig. Und das ist$$p(x) = \rho g x$$Wobei \(\rho \) die Dichte der Wassers ist und \(g\) die Erdbeschleunigung (Stünde der Zylinder auf dem Mond, wäre \(F\) kleiner!). \(b\) ändert sich auch mit \(x\); es wird ja mit wachsende \(x\) augenscheinlich kleiner. \(b\) lässt sich mit dem Phytagoras berechnen. \(b/2\), \(r\) und \(x\) bilden ein rechtwinkliges Dreieck$$\left( \frac b2 \right)^2 + x^2 = r^2 \implies b = 2 \sqrt{r^2 - x^2}$$ Jetzt alles für \(\text d F\) einsetzen und das Integral vorne anstellen:$$F = \int_{x=0}^r \rho g x \cdot 2 \sqrt{r^2 - x^2} \,\text d x$$Und das \(x\) verläuft von der Wasseroberfläche \(x=0\) bis zum tiefsten Punkt \(x=r\) des Kanals. Und auflösen$$\begin{aligned} F &= 2\rho g \int_{x=0}^r x \sqrt{r^2-x^2} \,\text d x \\ &= \left. -\frac 23\rho q \left( r^2 - x^2\right)^{\frac 32} \right|_{x=0}^r \\ &= \frac 23 \rho g r^3 \\ &\approx 6540 \frac{\text{kg}}{\text m^2 \text s^2} r^3 \approx 2243 \text N\end{aligned}$$Bei der Gelegenheit kann man dann auch gleich den Schwerpunkt des Kräftefeldes berechnen. Er liegt natürlich auf der Mittelachse, da das Ganze symmetrisch ist. Allgemein ist die Position \(x_S\) des Schwerpunkt $$x_S = \frac 1F \int x \cdot \text d F$$Das \(F\) und \(\text d F\) ist ja bereits bekannt$$\begin{aligned} x_S &= \frac 1F \int_{x=0}^r xp(x)b(x) \,\text d x \\ &= \frac{2 \rho g}{F} \int_{x=0}^r x^2 \sqrt{r^2-x^2} \,\text d x \\ &= \left. \frac{\rho g}{4F} \left( x (2x^2-r^2) \sqrt{r^2-x^2} + r^4 \arctan\left(\frac x{\sqrt{r^2-x^2}} \right)\right) \right|_{x=0}^r \\ &= \frac { \rho g r^4 \pi}{8F} = \frac {3 \pi}{16}r \\&\approx 0,589 \, r \approx 0,412 \, \text m\end{aligned}$$wenn Du also einen waagerechten Balken planst, der die Fläche fixieren soll, so sollte er sich genau so weit unterhalb der Wasseroberfläche befinden. Ich habe die Position der Kraft \(F\) im Bild oben eingezeichnet.
Noch ein Hinweis zu den Integralen. Das erste sollte man noch mit Hausmitteln lösen können. Ansonsten gibt es dafür Wolfram Alpha - aber das kennst Du sicher schon.
Falls Du noch Fragen hast, so melde Dich bitte. Achso - und die Kraft ist genau wie der Druck völlig unabhängig von der Länge des Kanals; siehe auch die Gleichung für den Druck.
Gruß Werner