Hallo Daniel,
mache Dir zunächst eine Skizze
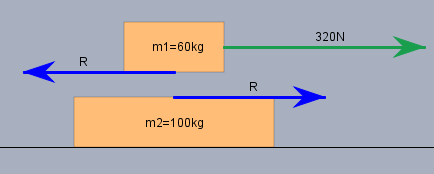
Ich habe die beiden Massen etwas aus einander gezogen, um die Reibkraft \(R\) zu verdeutlichen, die zwischen den Massen wirkt, wenn sie sich gegen einander bewegen. Zunächst gilt für die Masse \(m_1\):$$F_1 = m_1 \cdot a_1$$nun sind aber \(m_1\) und \(a_1\) bereits gegeben. Und \(F_1\) die Gesamtkraft, die auf \(m_1\) wirkt, setzt sich zusammen aus \(F_1=F-R\); folglich ist$$F -R = m_1 \cdot a_1 \\ \implies R = F - m_1 \cdot a_1 = 320\text{N} - 60\text{kg} \cdot 3 \frac{\text m}{\text s^2} = 140 \text N$$und für \(m_2\) gilt genauso$$F_2 = m_2 \cdot a_2 \\ \implies a_2 = \frac{F_2}{m_2} = \frac{R}{m_2} = \frac{140 \text N}{ 100 \text{kg}} = 1,4 \frac{\text m}{\text s^2}$$Da \(m_2\) zum Boden hin als reibungslos angenommen wird, ist \(R\) die einzige Kraft, die auf \(m_2\) wirkt.
Der Gleitreibungskoeffizient \(\mu\) ist$$\mu = \frac RG = \frac{R}{m_1 \cdot g} = \frac{140 \text N}{60 \text{kg} \cdot 9,81 \frac{\text m}{\text s^2}} \approx 0,24 $$Gruß Werner