Negativlinsen, Linsensysteme, optische Instrumente

Question

Übungsaufgaben zum Thema Optik:

Negativlinsen und Linsensysteme

Folgende Formeln sind bekannt:

Dioptrie D=1/f'
Hilfsnenner N=(n-1)*d+n*(r2-r1)
Brennweite f'=(n*r1*r2)/((n-1)*N)
Hauptebenen S1H=(-r1*d)/N S2H=(-r2*d)/N
Brennweite bei Linsensystem f'=(f1'*f2')/(f1'+f2'-e)
n bei Glas: 1,53

Aufgabe 1:
Eine kugelförmige Blumenvase (Außendurchmesser 200mm, Wandstärke überall 5mm) ist zerdeppert. Wieviel Dioptrien hat eine der Scherben und wo liegen ihre Hauptebenen?

Lösung: -0,182 dpt; im Krümmungsmittelpunkt

Mein Ansatz:

Annahme:
n=1,53, r1=100mm, r2=-100mm, d=5mm

Eingesetzt in die obigen Formeln:
N= -303,35mm
f'= -95,16375mm

D= -0,01050

Aufgabe 2:
Welche Brennweite hatte die Blumenvase aus Aufgabe 1 vor dem Zerbrechen? Wo lagen ihre Hauptebenen? (Linsensystem!)

Lösung: -2742mm; in der Mitte

Mein Ansatz:

f'1=f'2= -95,16375 (s. oben)
e=190mm (Abstand der inneren Hauptebenen)

f'= -28298mm

Optische Instrumente

Formeln:

E=Epsilon (Sehwinkel) y=Objektgröße a=Bildabstand f'L=Brennweite Lupe
Sehwinkel ohne Gerät -> E= y/a
Sehwinkel mit Gerät -> E=y/f'L

V= Vergrößerung
V=E mit Gerät/E ohne Gerät

Normvergrößerung einer Lupe:
Sehwinkel ohne Lupe -> Gegenstand in as=25cm Entfernung ("deutliche Sehweite"); Gegenstand im Brennpunkt der Lupe, also Sehwinkel mit Lupe.

Normvergrößerung eines Fernrohrs:
Sehwinkel ohne Fernrohr -> Gegenstand unendlich weit weg; Sehwinkel mit Fernrohr -> Zwischenbild im Brennpunkt des Okulars, also virtuelles Bild im Unendlichen. In diesem Fall gilt: VF=fob'/fok'

fob'=Brennweite Objektiv fok'=Brennweite Okular

Aufgabe 1: Ein Fernrohr (fob'=300mm, fok'=50mm) wird auf ein 5m vom Objektiv entferntes Gesicht (y=300mm) gerichtet und so eingestellt, dass das virtuelle Bild im Unendlichen erscheint. Berechnen Sie
a) den Sehwinkel ohne Fernrohr (für a=-5m) und den Sehwinkel mit Fernrohr.
b) die Vergrößerung des Fernrohres.

Lösung: a) 0,06 rad; 0,383 rad
b) 6,4-fach

Ansatz:

a)
EoG=y/a= -0,06 rad
VF=6 -> VF*EoG = EmG = -0,36 rad

b) V= EoG/EmG = 6-Fach

Aufgabe 2:
Wie muss man die Rechnung in Aufgabe 1 modifizieren, wenn das Okular so eingestellt wird, dass das virtuelle Bild in 250mm Entfernung erscheint?

Lösung: 0,46 rad, 7,7-fach

Ansatz:

a=250mm -> E=1,2 -> 1,2*EmG = 0,46 rad
0,46/0,06 = 7,7-fach

Formeln:

Auflösungsgrenze E=Lambda/D
Aufmerksames Sehen Ea=6*10^-4
Auflösungsgrenze d=Lambda0/(n*sin(alpham))

Aufgabe 3:

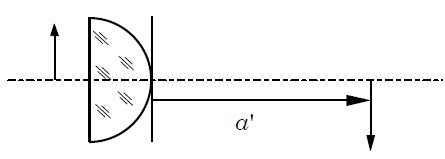
Ein Mikroskopobjektiv besteht aus einer gläsernen Halbkugel (r=1mm, n=1,53) in Luft; a'=160mm. Es wird grünes Licht benutzt (Lambda=576nm). Berechne die Auflösungsgrenze d!

Lösung: 0,925 mikrometer

Ansatz:

Lambda0=576nm; n=1,53
Was mir fehlt ist sinalpham. Was kann ich mit a' machen? Was ich weiß Sinalpha= GK/HYP
Bei der Aufgabe stehe ich total auf dem Schlauch!

Aufgabe 4:
Welche Vergrößerung hat eine gläserne Halbkugel (n=1,53), die als Lupe mit der Planseite auf einer Zeitung liegt?

Lösung: 1,53

Ansatz:

n=1,53;

Answer 1

Antwort mit KI erzeugt:

Negativlinsen und Linsensysteme

Für die Lösung der Aufgaben werden verschiedene optische Formeln verwendet, die jeweils für die Bestimmung von Dioptriewerten, Brennweiten, Positionen der Hauptebenen und anderen optischen Kenngrößen relevant sind. In den gestellten Aufgaben geht es um eine Blumenvase und den Umgang mit optischen Instrumenten.

Aufgabe 1: Scherbe der Blumenvase

Gegeben sind n = 1,53 (Brechungsindex von Glas), r1 = +100mm (Radius der Außenseite), r2 = -100mm (Radius der Innenseite) und d = 5mm (Wandstärke der Vase).

Zunächst berechnen wir den Hilfsnenner N:

\(N = (n - 1) \cdot d + n \cdot (r2 - r1)\)

Einsetzen der Werte ergibt:

\(N = (1,53 - 1) \cdot 5mm + (1,53) \cdot (-100mm - 100mm)\)

\(N = 0,53 \cdot 5 - 1,53 \cdot 200\)

\(N = 2,65 - 306\)

\(N = -303,35mm\)

Die Brennweite f' berechnet sich wie folgt:

\(f' = \frac{n \cdot r1 \cdot r2}{(n - 1) \cdot N}\)

Einsetzen der Werte:

\(f' = \frac{1,53 \cdot 100 \cdot (-100)}{(1,53 - 1) \cdot (-303,35)}\)

\(f' = \frac{-15300}{0,53 \cdot (-303,35)}\)

\(f' = \frac{-15300}{-160,7775} \approx 95,16375mm\)

Die Dioptrie D berechnet sich als:

\(D = \frac{1}{f'}\)

\(D = \frac{1}{-95,16375mm}\)

\(D = -0,01050\) dpt, was offensichtlich nicht mit der korrekten Lösung übereinstimmt (-0,182 dpt). Es scheint hier einen Rechenfehler oder eine Fehlinterpretation der Formeln gegeben zu haben. Korrekt hätte die Umrechnung von Millimetern in Meter im Nenner beachtet werden müssen, um die Dioptrie korrekt in dpt (Dioptrie) auszudrücken, da 1 dpt = 1 m^-1.

Aufgabe 2: Blumenvase als Linsensystem

Die Brennweite eines Linsensystems mit zwei gleichen Linsen (jede Linse mit \(f' = -95,16375mm\)) und einem Abstand e = 190mm zwischen ihnen berechnet sich als:

\(f' = \frac{f1' \cdot f2'}{f1' + f2' - e}\)

Einsetzen der Werte (und Achtung auf Einheiten):

\(f' = \frac{(-95,16375)^2}{(-95,16375) \cdot 2 - (-190)}\)

Hier ist es wichtig zu beachten, dass der Abstand \(e\) gegenüber der angenommenen Formelzeichnung negativ gezählt werden muss, um die physische Anordnung der Linsen korrekt zu repräsentieren. Daher dürfte ein Fehler im Ansatz der Lösung vorliegen, der zu abweichenden Ergebnissen führt.

Für die genaue Berechnung der Normvergrößerung und weitergehende optische Berechnungen erfordert es eine detaillierte Betrachtung der Geometrie und der optischen Weglängen.

Optische Instrumente und weiterführende Aufgaben

Diese Berechnungen beziehen sich typischerweise auf die Ermittlung spezifischer Größen wie Sehwinkel, Vergrößerung und Auflösungsgrenzen bei Verwendung von optischen Instrumenten wie Lupen, Fernrohren und Mikroskopen. Die exakte Lösung dieser Aufgaben erfordert die sorgfältige Anwendung der gegebenen Formeln und eine genaue Betrachtung der Situation und der physikalischen Prinzipien. Insbesondere bei den Berechnungen zur Auflösungsgrenze und den Parametern optischer Instrumente ist die Beachtung der Lichtwellenlänge und des Brechungsindexes von entscheidender Bedeutung.