Hallo Rellis,
Ich füge ein Koordinatensystem ein, dessen Ursprung im Schnittpunkt der Drehachse mit Boden der Zentrifuge liegt. \(y\) zeigt nach oben und \(x\) nach rechts.
Zunächst gilt es die Funktion \(y=f(x)\) der Kurve zu bestimmen, die den Schnitt mit der Wasserobfläche definiert. Dazu betrachte ich ein Wasserteilchen an der Oberfläche im Punkt \(P\).
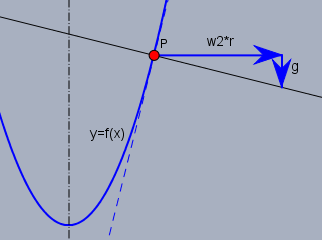
Die Oberfläche ist genau dann stabil, wenn die Summe aller Beschleunigungen auf das Wasserteilchen senkrecht zur Oberfläche steht. Die Beschleunigung setzt sich aus der Zentrifugal- (\(\omega^2 x\)) und der Erdbeschleunigung \(g\) zusammen. Folglich ist die Steigung \(y'\) der Funktion \(y=f(x)\) im Punkt \(P\)
$$y'(x) = \frac{\omega^2}{g}x$$ Daraus folgt zusammen mit \(y(0)=h_0\)
$$y(x)= \frac{\omega^2}{2g} x^2 + h_0$$ Der Einfachheit halber ersetze ich im folgenden \(\frac{\omega^2}{2g}\) durch \(a\). Umgekehrt gilt dann
$$x=\sqrt{\frac{1}{a}(y-h_0)}$$ womit sich dann das Volumen \(V\) des Rotationskörpers berechnen lässt.
$$V=\pi \int_{h_0}^{H} \left(x(y)\right)^2 \space dy= \frac{\pi}{2a} (H-h_0)^2$$ Aus der Forderung, dass die Wasseroberfläche den inneren Rand des Deckels erreichen soll, folgt:
$$y(\frac{d}{2}) = H \quad \Rightarrow \space H - h_0= a \frac{d^2}{4}$$ Das setze ich in die Gleichung für das Volumen ein
$$V= \frac{\pi}{2a} \cdot \left( a \frac{d^2}{4} \right)^2=\frac{\pi}{32}a d^4$$ Da das Volumen \(V\) identisch mit dem Freiraum oberhalb der Wasseroberfläche bei Stillstand der Zentrifuge sein muss - also \(V=(H-h) \pi \frac{D^2}{4}\) - lässt sich so der Wert für \(a\) und damit auch der Wert für \(\omega\) berechnen. Einsetzen von \(a\) in die Gleichung für \(y(\frac{d}{2})\) liefert den Wert für \(h_0\).