Hallo Schweizer,
Eine Skizze bringt mehr Klarheit:
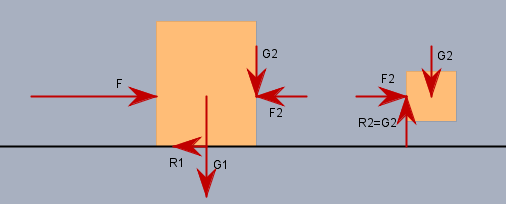
ich habe die beiden Klötze auseinander gezeichnet, damit ich die einzelnen Kräfte einzeichnen kann. Kräfte, die von \(K_1\) auf \(K_2\) wirken, wirken genauso umgekehrt (Actio gleich Reactio). Damit \(K_2\) nicht fällt, muss die Reibung \(R_2\) das Gewicht \(G_2\) halten. Also ergibt sich für die Kraft \(F_2\) zwischen den Klötzen
$$F_2 = \frac{1}{\mu_2} G_2 = \frac{1}{\mu_2} \cdot m_2 \cdot g$$ um eine Kraft \(F_2\) zu generieren, ist eine Beschleunigung \(a\) nötig - mit \(F_2 = m_2 \cdot a\). \(a\) ist natürlich auch die gemeinsame Beschleunigung des Gesamtsystems.
$$a = \frac{F_2}{m_2} = \frac{g}{\mu_2}$$ Die Reibung \(R_1\), die gegen die Bewegung von \(K_1\) wirkt, ist
$$R_1 = (G_1 + G_2)\mu_1 = (m_1 + m_2)g \cdot \mu_1$$ Die Summe aller horizontalen Kräfte an \(K_1\) und \(K_2\) gibt die horizontale Beschleunigung \(a\) von \(m_1+m_2\) - also
$$ a \cdot (m_1 +m_2) = F - R_1 \quad \Rightarrow F = a \cdot (m_1 +m_2) + R_1$$
Einsetzen von \(a\) und \(R_1\) ergibt dann
$$ \begin{aligned} F &= \frac{g}{\mu_2} \cdot (m_1 +m_2) + (m_1 + m_2)g \cdot \mu_1 \\ &= \left( \frac{1}{\mu_2} + \mu_1\right)(m_1 + m_2)g \\ &= \left( \frac{1}{0,6} +0,4\right)(2,5 \text{kg} + 0,5\text{kg})\cdot 9,81 \frac{\text{m}}{\text{s}^2} \\& \approx 60,8 \text{N}\end{aligned}$$ Gruß Werner