Flächenträgheitsmoment, gleichseitiges Dreieck

Question

Flächenträgheitsmoment:

Wenn I_yy für das gleichseitige Dreieck 1/(2*Wurzel(3) ) a⁴ beträgt, hat I_zz den selben Wert wegen der Symmetrie oder doch nicht? Wenn nicht, wie lautet dann der Wert für I_zz?

Answer 1

Hallo probe,

schaue doch die Flächenträgheitsmomente einfach nach. Unter dem Wikipedia-Eintrag findest Du den Wert für \(I_{y}\) (\(s\) sei die Länge einer Seite des gleichseitigen Dreiecks und \(h=\frac12 \sqrt{3}s\))

$$I_{y}=\frac{s \cdot h^3}{36} = \frac{s \cdot 3\sqrt{3} \cdot s^3}{36 \cdot 8} = \frac{s^4}{4\cdot \sqrt{3} \cdot 8} = \frac{1}{2\sqrt{3}} \left( \frac{s}{2}\right)^4$$ Also ist Dein \(a\) aus der Aufgabe ist \(a=\frac{s}{2}\). Das Flächenträgheitsmoment \(I_z\) ist

$$I_z= \frac{h \cdot s^3}{48} = \frac{\sqrt{3} s^4}{2 \cdot 48} = \frac{\sqrt{3} \cdot 16 a^4}{2 \cdot 48} = \frac{1}{2\sqrt{3}}a^4$$ Ist also genauso groß. Ich würde sagen, nicht offensichtlich auf Grund der Symmetrie .... eher 'zufällig'.

Gruß Werner

Comments

Vielen Dank.

Wenn man den Schwerpunkt bestimmen soll, für eine Fläche, bei dem ein Kreis ausgeschniten wurde. Das heißt dann, dass beim Tabellenverfahren nur die Fläche für den Kreis ein negatives Vorzeichen bekommt, der Rest bleibt wie er immer bleiben muss oder?

Wie ist es beim Flächenträgheitsmoment, was bekommt jetzt alles ein negatives Vorzeichen?

------

Also mir geht es jetzt nur darum, wenn eine Fläche ausgeschnitten wird, sozusagen ein Loch hat... Was sich dann beim Schwerpunkt & Flächenträgheitsmoment verändert...

Das allgemeine Prinzip wo nichts ausgeschnitten ist, ist mir schon klar.

----

Ich hoffe Du verstehst was ich meine...

---

"Das heißt dann, dass beim Tabellenverfahren nur die Fläche für den Kreis ein negatives Vorzeichen bekommt, der Rest bleibt wie er immer bleiben muss oder?" ohne zu wissen was ein Tabellenverfahren ist, würde ich dem trotzdem zustimmen. Löcher werden einfach durch negative Vorzeichen berücksichtigt.

"Also mir geht es jetzt nur darum, wenn eine Fläche ausgeschnitten wird, sozusagen ein Loch hat... Was sich dann beim Schwerpunkt & Flächenträgheitsmoment verändert..." Schwerpunkt und auch Flächenträgheitsmoment lassen sich beide über eine Summe bzw. ein Integral bestimmen. Ein Integral ist letztlich auch nur eine Summe (mit unendlich vielen Summanden). Das bedeutet umgekehrt, dass Du in beiden Fällen 'Löcher' über ein negatives Vorzeichen berücksichtigen kannst. Beispiel

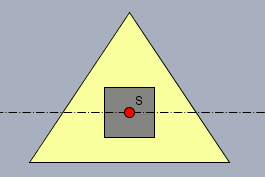
Das Flächenträgheitsmoment um die eingezeichnete (Y-)Achse der gelben Fläche ist allgemein

$$I_y= \int_{\colorbox{#ffff00}{A}}x \;\text{d}A$$ oder eben

$$I_y= \int_{\colorbox{#ffff00}{A}} z^2 \;\text{d}A= \int_Dz^2 \;\text{d}D - \int_{\colorbox{#848484}{Q}} z^2 \;\text{d}Q$$ wobei \(D\) die Fläche des Dreiecks und \(Q\) die Fläche des Quadrats ist.