Hallo,
Du weißt, dass die Stäbe nur Kräfte in Stabrichtung aufnehmen können. Steht also der Stab 1 in einem Winkel von \(\alpha_1\) zur Horizontalen so ist die Kraft \(\vec{S}_1\) in 1:
$$\vec{S}_1 = \begin{pmatrix} \cos \alpha_1\\ \sin \alpha_1\end{pmatrix} \cdot |S_1|$$ man könnte aber genauso gut schreiben, da die Richtung durch die Geometrie des Fachwerks vorgegeben ist:
$$\vec{S}_1 = \begin{pmatrix} 1,75 \\ 1,2\end{pmatrix} \cdot t_1$$ und \(t_1\) ist halt irgendein Faktor. Schau Dir nun folgende Skizze an.
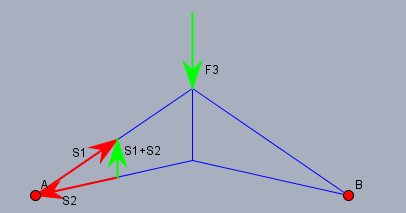
Dort habe ich die beiden Stabkräfte (rot) und ihre Summe (grün) am Punkt \(A\) eingezeichnet. Ich habe die Kräfte gleich in ihren zu erwartenden Richtungen eingezeichnet. S1 ist ein Druck- und S2 ein Zugstab. Die Summe muss \(=-\frac12 \vec{F}_2\) sein, da beide Stäbe zusammen die Hälfte der Kraft \(\vec{F}_2\) an der Spitze des Fachwerks aufnehmen muss. Die Kräfte \(\vec{F}_1\) und \(\vec{F}_3\) spielen für die Stäbe keine Rolle! Folglich muss gelten:
$$\vec{S}_1 + \vec{S}_2 = -\frac{1}{2} \vec{F}_2$$
$$\begin{pmatrix} 1,75 \\ 1,2\end{pmatrix} \cdot t_1 + \begin{pmatrix} -1,75 \\ -0,4\end{pmatrix} \cdot t_2 = \begin{pmatrix} 0 \\ 4 \text{kN}\end{pmatrix}$$ das sind zwei Gleichungen in X- und Y-Richtung. Aus der ersten folgt direkt, dass \(t_1=t_2\) ist. Folglich ist
$$1,2 t_1 - 0,4t_1 = 4 \text{kN} \quad \Rightarrow t_1 = 5\text{kN}$$
$$\vec{S}_1 = \begin{pmatrix} 1,75 \\ 1,2\end{pmatrix} 5\text{kN} = \begin{pmatrix} 8,75 \\ 6\end{pmatrix} \text{kN} \quad \Rightarrow |\vec{S}_1| \approx 10,6 \text{kN}$$
$$\vec{S}_2 = \begin{pmatrix} -1,75 \\ -0,4\end{pmatrix} 5\text{kN} = \begin{pmatrix} -8,75 \\ -2\end{pmatrix} \text{kN} \quad \Rightarrow |\vec{S}_2| \approx 9,0 \text{kN}$$
Die Kräfte in 4 und 5 sind aus Gründen der Symmetrie genauso groß bzw. symmetrisch. Und die Kraft in Stab 3 bekommt man über das Kräftegleichgewicht im unteren Knoten von Stab 3. Es gilt hier:
$$-\vec{S}_2 + \vec{S}_3 - \vec{S}_4= 0 $$
Hier müssen die Kräfte für 2 und 4 negativ angesetzt werden, da sie ja auf der 'anderen Seite' des Stabs auf den Stab wirken!
$$ \begin{aligned} \Rightarrow \vec{S}_3 &= \vec{S}_2 + \vec{S}_4 \\ &= \begin{pmatrix} -8,75 \\ -2\end{pmatrix} \text{kN} + \begin{pmatrix} +8,75 \\ -2\end{pmatrix} \text{kN} \\ &= \begin{pmatrix} 0 \\ -4\end{pmatrix} \text{kN} \end{aligned}$$ Die Kraft \(\vec{S}_3\) zeigt nach unten, d.h. vom Stab weg. Stab 3 ist also ein Zugstab.
Gruß Werner
PS.: ich freue mich immer über Feedback. Was ist denn aus Deiner Übung zur Mechanik geworden?