Zerlegung von Kräften: An einem Handwagen ziehen 2 Personen in unterschiedlichem Winkel

Question

Hallo zusammen,

ich schreibe demnächst meine Physik-Prüfung und habe noch ein paar offene Fragen, bei denen ihr mir hoffentlich helfen könnt ;)

>>> An einem Handwagen zieht eine Person im Winkel von 20° zur Fahrtrichtung mit F=500N und eine zweite Person im Winkel von 30° zur Fahrtrichtung nach der anderen Seite mit F=1200N. Bestimmen Sie die Größe und Richtung der resultierenden Kraft!

(Ergebnis: F_res=1575 N, 16° zur Fahrtrichtung)

Comments

Bitte mit Erklärung zum Lösungsweg ;)

Answer 1

Zunächst eine Skizze:

 

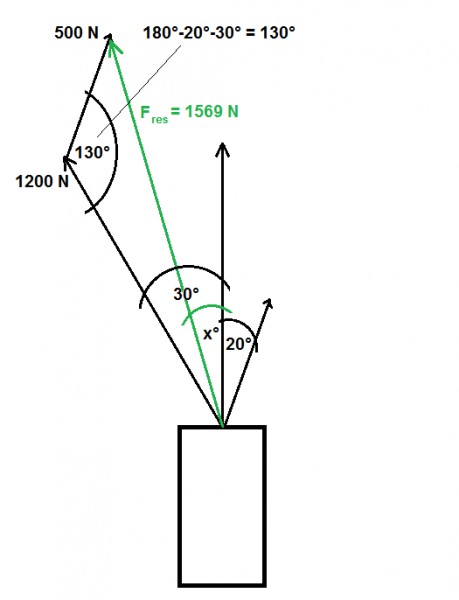
Den Betrag der resultierenden Kraft F_res kann man mit dem Kosinussatz berechnen:

F_res² = 500 ² + 1200 ² - 2 * 500 * 1200 * cos ( 130 ° ) 

<=> F_res = √ ( 500 ² + 1200 ² - 2 * 500 * 1200 * cos ( 130 ° ) ) = 1569 N

 

Auch die Richtung von F_res kann man mit einer Umformung des Kosinussatzes berechnen. Es gilt (siehe auch Skizze):

1200 ² = 500 ² + 1569 ² - 2 * 500 * 1569 * cos ( 20 + x )

<=> cos ( 20 + x ) = ( 1200 ² - 500 ² - 1569 ² ) / ( - 2 * 500 * 1569 )

<=> x = arccos ( ( 1200 ² - 500 ² - 1569 ² ) / ( - 2 * 500 * 1569 ) ) - 20 = 15,85 °

 

So ungefähr stimmt das ja mit der vorgegebenen Lösung überein. Die geringen Abweichungen können auf Rundungen der Musterlösung beruhen. Ich habe allerdings nur die Ergebnisse gerundet, keine Zwischenergebnisse.