Hallo Fedel,
a) Die Wirkungsweise kannst Du bei Wikipedia lesen. Ein Transformator kann nicht mit Gleichspannung betrieben werden, da es bei konstantem Strom zu keiner Änderung des Magnetischen Feldes im Sekundärkreis kommen würde. Und ohne diese Änderung wird auch keine Spannung in der Sekundärspule induziert.
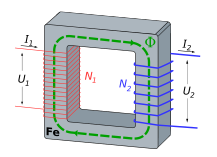
b) Bei einem idealen Transformator verhalten sich die Spannungen wie die Anzahl der Windungen.
$$\frac{U_2}{U_1} = \frac{N_2}{N_1}$$Bei \(U_2=230\text{V}\), \(N_1=600\) und \(U_2=9\text{V}\) gibt das
$$N_2 = \frac{U_2}{U_1} \cdot N_1 = \frac{9}{230} \cdot 600 \approx 23,48$$ Es heißt "runden Sie sinnvoll"! rein mathematisch würde man auf 23 runden. Da in der Praxis aber immer mit Verlusten zu rechnen ist, würde ich auf 24 runden.
$$N_2=24$$
c) Die Ströme verhalten sich beim idealen Transformator umgekehrt zu den Anzahlen der Wicklungen. D.h.:
$$\frac{I_2}{I_1} = \frac{N_1}{N_2}$$ in diesem Fall (\(N_2=10\)) wäre dann
$$I_2 = \frac{N_1}{N_2} \cdot I_1 = \frac{600}{10} \cdot 0,42\text{A} = 25,2 \text{A} $$
d) Die Leistung \(P_1\), die in den Primärkreis hineingeht, kommt beim Sekundärkreis wieder heraus (\(P_2\)) - multipliziert mit dem Wirkungsgrad \(\eta = 90\%\).
$$P_2 = \eta \cdot P_1 = \eta \cdot U_1 \cdot I_1 = 0,9 \cdot 230 \text{V} \cdot 0,42 \text{A} = 86,94\text{W}$$
Gruß Werner
Edit: \(\eta\) von \(95\%\) auf \(90\%\) korrigiert.